Yarn Strength Prediction: A Practical Model Based on Artificial Neural Networks

논문 정보

• 제목: Yarn Strength Prediction: A Practical Model Based on Artificial Neural Networks
• 저자: Rocco Furferi (University of Florence), Maurizio Gelli (New Mill S.P.A. Research Center)
• 학회/저널: Advances in Mechanical Engineering
• 발행일: 2010-06-17
• DOI: 10.1155/2010/640103
• 주요 연구 내용: 원사 강도 예측을 위해 피드포워드 역전파 인공신경망(FFBP ANN) 모델을 개발함. 이 모델은 전문가들이 통상적으로 측정하는 5가지 로빙 파라미터(원사 번수, 꼬임 수, 가중 평균 길이, 가중 평균 섬도, 가중 평균 강도)를 입력으로 사용하여 최종 원사의 강도를 예측함.
• 주요 결과 및 결론: 개발된 ANN 모델을 98개의 데이터로 학습하고 50개의 새로운 데이터로 검증한 결과, 평균 예측 오차율 3.5%를 달성함. 이는 동일 데이터로 구축한 다중 선형 회귀 모델의 평균 오차율 5.55%보다 훨씬 우수한 성능임.
• 기여점: 섬유 공정 전문가들이 실제 방적을 수행하기 전에 원사 강도를 빠르고 정확하게 예측할 수 있는 실용적인 도구를 제공함. 이를 통해 다양한 로빙 조합을 신속하게 테스트하여 시간과 비용을 절감하고, 최적의 원사 품질을 확보하는 데 기여함.

요약

초록

원사 강도는 방적 공정에서 관리해야 할 가장 중요한 매개변수 중 하나로, 로빙의 특성과 방적 공정에 크게 의존한다. 기존에는 전문가의 경험에 의존해 원사 강도를 정성적으로 예측했으나, 원하는 강도를 얻기까지 많은 테스트가 필요했다. 이 연구는 피드포워드 역전파 인공신경망(FFBP ANN)을 기반으로, 실제 방적 없이 로빙 파라미터만으로 원사 강도를 신뢰성 있게 예측하는 모델을 제안한다. 98개의 데이터로 모델을 학습하고 50개의 새로운 데이터로 검증한 결과, 평균 예측 오차는 4% 미만이었으며, 이는 다중 회귀 분석보다 우수한 결과이다.

서론

원사 강도는 방적 공정의 품질을 결정하는 핵심 지표이다. 전문가들은 섬유의 강도, 길이, 꼬임 수, 번수, 섬도 등을 종합하여 강도를 예측하지만, 이는 경험에 의존하는 부정확한 방식이다. 원사 강도와 섬유 특성 간의 관계는 비선형적이기 때문에 기존의 선형 회귀 모델로는 정확한 예측이 어렵다. 이러한 비선형 관계를 모델링하기 위해 인공지능, 특히 인공신경망(ANN) 접근법이 효과적이다. 본 연구는 현장 전문가들이 일반적으로 측정하는 로빙 파라미터를 사용하여 원사 강도를 예측하는 실용적인 ANN 모델 개발을 목표로 한다.

모델 아키텍처 / 방법론

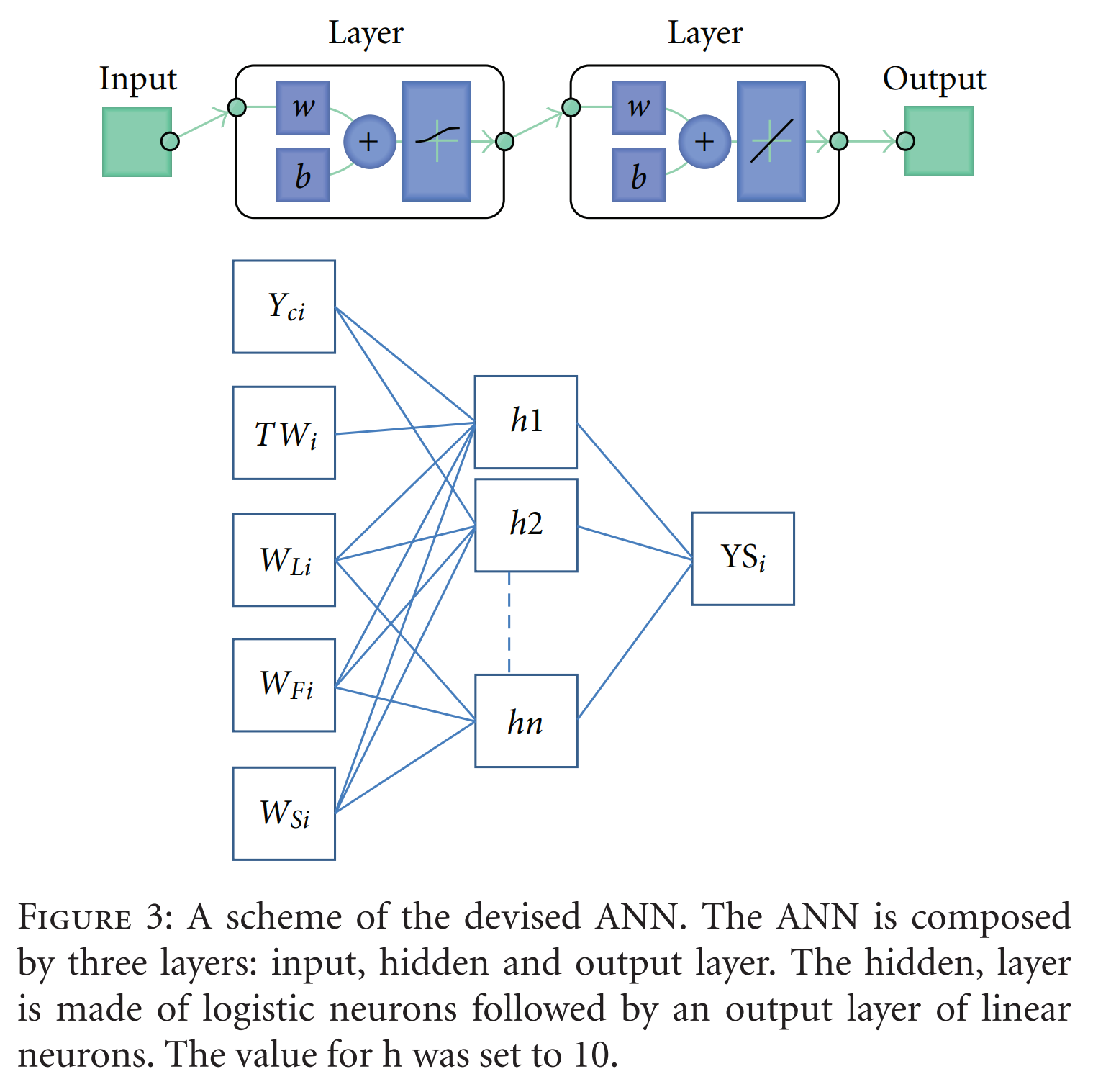
• 핵심 구조/방법: 연구의 핵심은 실험 데이터를 기반으로 FFBP ANN 모델을 구축하고 훈련시키는 것이다. 총 6가지 종류의 로빙을 사용하여 98개의 실험 데이터를 생성했다. 각 로빙을 구성하는 섬유들의 특성(비율, 길이, 굵기, 강도)과 공정 변수(사번, 꼬임 수)를 조합하여 5개의 입력 파라미터를 정의하고, 이를 통해 측정된 방적사 강도를 예측하도록 모델을 설계했다.
• 주요 구성 요소: 논문의 Figure 3에서 제시된 모델 구조는 3개의 계층으로 구성된다.
  • 입력층: 5개의 뉴런 (사번 $Y_c$, 꼬임 수 $T_w$, 가중 평균 길이 $W_L$, 가중 평균 굵기 $W_F$, 가중 평균 강도 $W_S$)
  • 은닉층: 10개의 로지스틱 뉴런
  • 출력층: 1개의 선형 뉴런 (예측된 방적사 강도 $YS_{predicted}$)
• 수식: 입력 데이터 계산을 위해 다음과 같은 가중 평균 수식이 사용되었다. 로빙을 구성하는 i번째 섬유의 비율을 $\alpha_i$, 길이를 $L_i$, 굵기를 $F_i$, 강도를 $R_i$라고 할 때 각 가중 평균값은 다음과 같다.
  • 가중 평균 길이: $W_L = \sum \alpha_i L_i$
  • 가중 평균 굵기: $W_F = \sum \alpha_i F_i$
  • 가중 평균 강도: $W_S = \sum \alpha_i R_i$
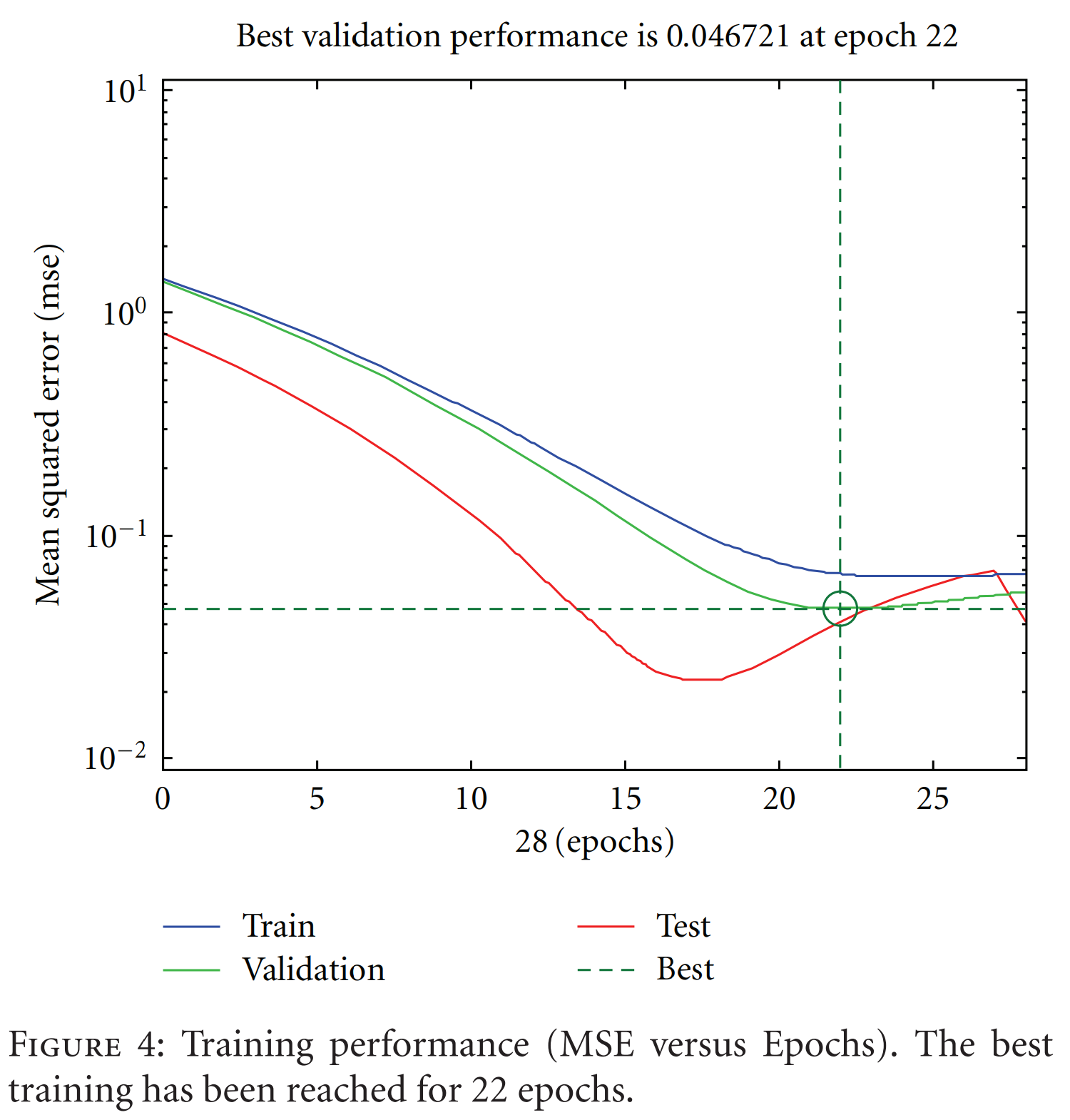
• 알고리즘: 모델 훈련은 Levenberg-Marquardt 역전파 알고리즘을 사용했다. 과적합을 방지하기 위해 조기 종료(early stopping) 기법이 적용되었으며, 훈련 과정의 성능 그래프(Figure 4)에 따르면 22번째 epoch에서 최적의 검증 성능에 도달하여 훈련이 중지되었다.

실험 결과

• 주요 데이터셋: 6가지 로빙군으로부터 수집된 98개의 샘플을 훈련 데이터셋으로 사용했다. 모델의 성능 검증을 위해 별도로 50개의 새로운 로빙 샘플을 테스트 데이터셋(검증 세트)으로 사용했다.
• 핵심 성능 지표: 모델의 예측 정확도는 예측 오차($\eta$)로 평가되었다. 50개의 검증 세트에 대한 실험 결과, ANN 모델의 **평균 예측 오차는 3.5%**였고 표준편차는 0.015로 나타났다. 이는 매우 안정적이고 정확한 예측 성능을 보여준다.
• 비교 결과: 제안된 ANN 모델의 성능을 전통적인 통계 기법인 다중 선형 회귀 모델과 비교했다. 동일한 데이터셋을 사용했을 때, 다중 선형 회귀 모델의 **평균 예측 오차는 5.55%**로, ANN 모델의 오차율(3.5%)보다 약 2%p 더 높았다. 이는 방적사 강도 예측 문제의 비선형성을 ANN이 더 효과적으로 모델링했음을 시사한다.

결론

본 연구에서 개발된 FFBP ANN 모델은 로빙의 물리적 특성만으로 방적사의 강도를 신속하고 신뢰성 있게 예측하는 실용적인 방법을 제공한다. 이 모델은 기술자들이 시간과 비용이 많이 드는 물리적 방적 테스트를 생략하고도 다양한 원료 배합의 결과를 미리 시뮬레이션할 수 있게 해준다. 결과적으로, 원하는 품질의 원사를 생산하기 위한 의사결정 과정을 단축하고 생산 효율성을 높이는 데 기여할 수 있다. 현재 이 모델은 실제 섬유 회사(New Mill S.p.A.)의 연구소에서 활용되고 있다.