Skip to main content

Combining some Biased Estimation Methods with Least Trimmed Squares Regression and its Application

· 5 min read
Betül Kan-Kılınç
연구원
Ozlem Alpu
연구원

논문 정보​

  • 제목: Combining some Biased Estimation Methods with Least Trimmed Squares Regression and its Application
  • 저자: Betül Kan-Kılınç (Anadolu University), Ozlem Alpu (Eskisehir Osmangazi University)
  • 학회/저널: Revista Colombiana de Estadística
  • 발행일: 2015-07-01
  • DOI: 10.15446/rce.v38n2.51675
  • 주요 연구 내용: 회귀분석에서 다중공선성(multicollinearity)과 이상치(outlier) 문제가 동시에 발생할 때, 기존의 최소자승법(OLS)은 신뢰할 수 없는 결과를 낳는다. 이 연구는 이 두 문제를 동시에 해결하기 위해 강건 회귀(robust regression) 방법인 LTS(Least Trimmed Squares)와 다중공선성 해결을 위한 편향 추정(biased estimation) 방법인 Ridge 및 Liu 회귀를 결합하는 접근법을 제안한다. 또한, 이러한 강건 편향 추정법을 쉽게 적용하고 비교할 수 있는 R 패키지 ltsbase를 개발하여 소개한다.
  • 주요 결과 및 결론: 이상치를 포함하는 두 개의 실제 데이터셋(hbk, toxicity)을 대상으로 제안된 방법을 실험한 결과, LTS 기반의 Liu 추정법(LTS-Liu)이 OLS, Ridge, Liu, LTS-Ridge 등 다른 방법들보다 일관되게 가장 낮은 평균 제곱 오차(MSE)를 기록했다. 이는 다중공선성과 이상치가 공존하는 데이터에서 제안된 강건 편향 추정법이 매우 효과적임을 입증하며, 개발된 ltsbase 패키지가 실용적인 분석 도구로서의 가치가 있음을 보여준다.
  • 기여점: 다중공선성과 이상치 문제를 동시에 다루는 강건 편향 추정법(LTS-Ridge, LTS-Liu)의 효과성을 실증적으로 검증했다. 이 방법론을 사용자가 편리하게 이용할 수 있도록 R 패키지 ltsbase를 개발하고 그 기능을 상세히 소개하여 관련 연구 및 분석의 접근성을 높였다.

요약​

초록​

회귀분석에서 다중공선성과 이상치가 함께 존재할 경우, 분석가는 두 문제를 동시에 처리해야 한다. 이런 상황에서는 강건 추정량에 기반한 편향 추정 방법이 회귀 계수를 추정하는 데 유용하다. 이 연구에서는 문헌에 알려진 데이터셋(x 방향 이상치, x와 y 양방향 이상치 포함)에 대해 R 패키지 ltsbase를 사용하여 여러 강건 편향 추정량을 검토한다. 이 패키지의 기능과 특성을 활용하여 강건 편향 추정량의 성능을 평가한다.

서론​

경제, 기술, 의료 등 다양한 분야에서 다중공선성은 흔한 문제이며, 여기에 이상치까지 더해지면 표준적인 회귀분석 방법은 한계를 보인다. 기존의 최소자승법(OLS)은 이상치에 민감하고 다중공선성 존재 시 계수 추정치의 분산이 매우 커져 불안정해진다. 이 문제를 해결하기 위해, 다중공선성을 완화하는 Ridge, Liu 같은 편향 추정법과 이상치의 영향을 줄이는 LTS 같은 강건 추정법을 결합하는 연구가 필요하다. 이 논문은 두 방법을 결합한 강건 편향 추정법의 성능을 평가하고, 이를 쉽게 구현할 수 있는 ltsbase라는 R 패키지를 소개하는 것을 목표로 한다.

배경​

  • LTS (Least Trimmed Squares): Peter Rousseeuw에 의해 소개된 강건 회귀 기법이다. 잔차의 제곱합을 최소화하는 대신, 오름차순으로 정렬된 잔차 제곱값 중 가장 작은 hh개의 합을 최소화한다 (n/2≤h≤nn/2 \le h \le n).

    • 목적 함수: minβ∑i=1h(e2)i:nmin_{\beta}\sum_{i=1}^{h}(e^{2})_{i:n}
    • 이 방식은 잔차가 큰 (n−h)(n-h)개의 이상치를 추정 과정에서 효과적으로 제외하므로 이상치에 강건한 추정치를 제공한다.

  • 다중공선성 (Multicollinearity): 설명 변수들 간에 강한 선형 관계가 존재하는 현상이다. 이로 인해 OLS 추정량의 분산이 커져 계수 추정이 불안정해진다. 진단을 위해 주로 분산팽창계수(VIF)와 상태수(Condition Number)를 사용한다.

    • VIF: VIF=1/(1−Ri2)VIF = 1/(1-R_i^2), 일반적으로 10 이상이면 다중공선성을 의심한다.
    • 상태수: λmax/λmin\lambda_{max}/\lambda_{min}, 1000 이상이면 심각한 다중공선성을 의미한다.

  • 편향 추정법 (Biased Estimators): 다중공선성 문제 해결을 위해 OLS 추정량에 약간의 편향(bias)을 허용하는 대신 분산을 크게 줄이는 방법이다.

    • Ridge 회귀: β^Ridge=(X′X+kI)−1X′y\hat{\beta}_{Ridge}=(X^{\prime}X+kI)^{-1}X^{\prime}y (k>0k>0)
    • Liu 회귀: βLiu=(X′X+I)−1(X′X+dI)β‾\beta_{Liu}=(X^{\prime}X+I)^{-1}(X^{\prime}X+dI)\overline{\beta} (0<d<10<d<1)
    • kk와 dd는 편향 파라미터로, 모델의 복잡도를 제어하는 역할을 한다.

모델 아키텍처 / 방법론​

Figure 2 Figure 4

  • 핵심 구조/방법: 이 연구의 핵심은 LTS 추정법을 기반으로 Ridge와 Liu 편향 추정법을 결합한 것이다. 즉, 기존 OLS 기반의 편향 추정 모델의 구성요소를 LTS 기반의 강건한 통계량으로 대체하여 β^ltsRidge\hat{\beta}_{ltsRidge}와 β^ltsLiu\hat{\beta}_{ltsLiu}를 추정한다.
  • 주요 구성 요소:
    • ltsbase R 패키지: 제안된 방법론을 구현한 핵심 도구다. OLS, Ridge, Liu, LTS, LTS-Ridge, LTS-Liu 모델을 모두 계산하고, 최소 평균 제곱 오차(MSE)를 기준으로 최적의 모델과 편향 파라미터(kltsk_{lts}, dltsd_{lts})를 찾아준다.
    • 성능 평가 지표: 모델의 성능은 평균 제곱 오차(MSE)를 기준으로 평가된다.
      • MSE(β^∙)=trCov(β^∙)+bias(β^∙)′bias(β^∙)MSE(\hat{\beta}_{\bullet})=trCov(\hat{\beta}_{\bullet})+bias(\hat{\beta}_{\bullet})^{\prime}bias(\hat{\beta}_{\bullet})
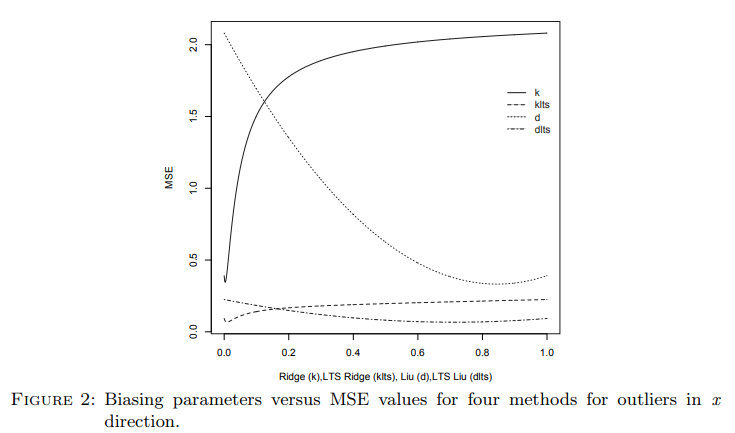
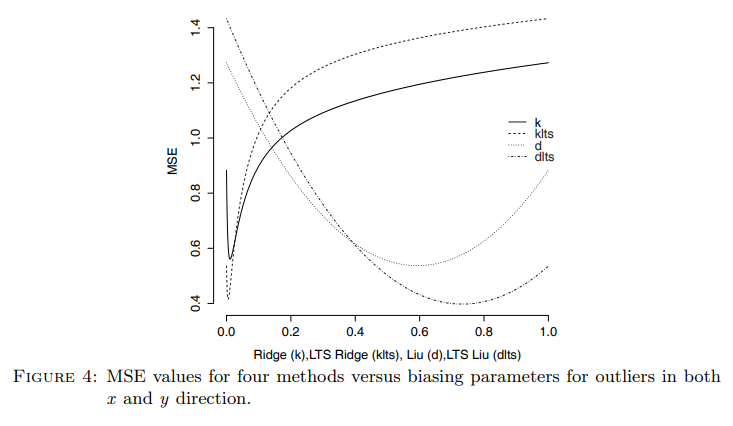
  • 알고리즘: ltsbase 패키지는 사용자가 지정한 범위 내에서 편향 파라미터(k,dk, d)를 바꿔가며 각 모델의 MSE를 계산한다. 그 후, 최소 MSE를 갖는 모델의 회귀 계수와 편향 파라미터 값을 결과로 반환한다. 또한, MSE 값의 변화를 시각화하는 그래프를 제공하여 직관적인 비교를 돕는다. 논문의 Figure 2와 Figure 4는 이러한 비교 그래프의 예시를 보여준다.

실험 결과​

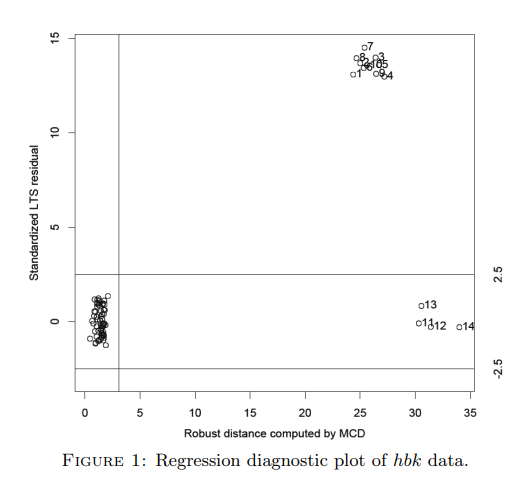
Figure 1 Figure 3

  • 주요 데이터셋:
    1. hbk 데이터: 75개의 관측치와 3개의 설명 변수로 구성된 인공 데이터셋. x 방향으로 높은 레버리지(leverage)를 갖는 이상치를 포함한다.
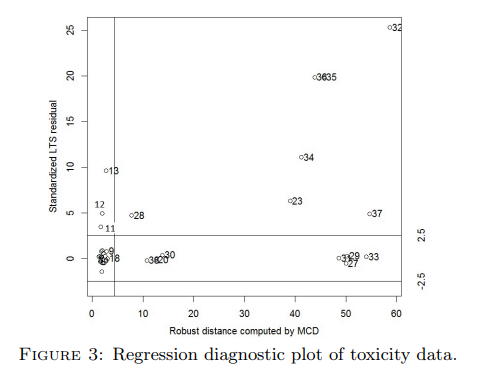
    2. toxicity 데이터: 38개의 관측치와 9개의 설명 변수로 구성된 실제 데이터셋. x와 y 양방향으로 이상치를 포함하며 심각한 다중공선성 문제를 가지고 있다.
  • 핵심 성능 지표:
    • hbk 데이터 분석: LTS-Liu 방법이 MSE 0.067을 기록하여 OLS(0.391), LTS-Ridge(0.068) 등 다른 모든 방법을 능가하는 최고의 성능을 보였다. 이때 최적의 편향 파라미터 dltsd_{lts}는 0.673이었다. 논문의 Figure 1은 hbk 데이터의 이상치를 시각적으로 보여준다.
    • toxicity 데이터 분석: 이 데이터셋에서도 LTS-Liu 방법이 MSE 0.398로 가장 우수한 성능을 나타냈으며, OLS(0.883), LTS-Ridge(0.561)보다 월등히 낮은 오차를 기록했다. 최적의 dltsd_{lts}는 0.712였다. 논문의 Figure 3은 toxicity 데이터의 이상치 분포를 보여준다.
  • 비교 결과: 두 실험 모두에서, 다중공선성과 이상치가 공존하는 상황에서는 표준적인 방법(OLS, Ridge, Liu)보다 LTS를 결합한 강건 편향 추정법이 훨씬 우수한 예측 성능을 보였다. 특히 LTS-Ridge보다 LTS-Liu의 성능이 일관되게 더 좋게 나타났다.

결론​

이 연구는 다중공선성과 이상치가 동시에 존재하는 데이터에 대해 Ridge 및 Liu 편향 추정법과 LTS 강건 추정법을 결합하는 것이 매우 효과적인 해결책임을 입증했다. 연구를 통해 개발된 ltsbase R 패키지는 이러한 복합적인 문제를 다루는 데 필요한 모델링 및 비교 분석 기능을 통합적으로 제공함으로써, 기존 R 환경의 분석 도구 공백을 메우는 중한 기여를 한다. 이 패키지는 사용자가 강건 편향 회귀 모델을 쉽게 적용하고, MSE를 기준으로 최적의 모델을 선택할 수 있도록 지원하여 데이터 분석의 실용성과 신뢰성을 높인다.