Skip to main content

통계적 해석 방법과 모델 기반 방법을 사용한 차원축소: Elementary effect 기법과 random forest regressor 의 비교

· 5 min read
정인범
한양대학교 석사

논문 정보​

  • 제목: Dimensionality reduction using statistical analysis and model based methods: a comparison between elementary effect method and random forest regressor
  • 저자: 정인범 (한양대학교 대학원)
  • 학회/저널: 한양대학교 대학원 석사학위논문
  • 발행일: 2018-02
  • DOI: (N/A, URI: 1804:null-200000432990)
  • 주요 연구 내용: 본 연구는 차원축소 기법을 변수선택(Filter, Wrapper, Embedded)과 변수추출(PCA, Autoencoder)로 분류함. 이후 통계적 해석(Filter) 방법인 Elementary Effect(EE) 기법과 모델 기반(Embedded) 방법인 Random Forest Regressor(RFR)의 변수 중요도 계산 방식과 성능을 비교 분석함.
  • 주요 결과 및 결론: 시뮬레이션 모델(데이터 생성 필요)의 경우, EE 기법(특히 Sampling for Uniformity)이 RFR보다 적은 해석 횟수로 높은 변수 선별 정확도를 보였음. 반면, 'Big data'와 같이 이미 데이터가 확보된 경우 RFR이 더 적합했음. 또한 RFR은 변수추출 기법인 Autoencoder보다 사용이 편리하고 우수한 성능을 보임.
  • 기여점: 서로 다른 학문적 배경(통계적 GSA vs. 기계학습)에서 발전한 두 주요 차원축소 기법(EE, RFR)의 성능을 정량적으로 비교, 분석하였음. 데이터 상황(시뮬레이션 vs. 기존 데이터)에 따라 적절한 기법을 선택해야 함을 실증적으로 제시함.

요약​

초록​

공학 설계에서 변수 증가로 인한 과도한 전산 비용을 방지하기 위해, 스크리닝 기법으로 변수 중요도를 계산하고 불필요한 변수를 제외한다. 과거에는 ANOVA 같은 통계 기법이 사용되었으나, 데이터와 변수 개수가 증가하며 더 효과적인 방법이 개발되었다. 이러한 차원축소 기법은 변수선택과 변수추출로 나뉜다. 변수선택은 기준을 만족하는 변수의 부분집합을 찾고, 변수추출은 새로운 변수 집합을 정의한다. 본 논문은 변수선택 방법 중 통계적 Filter 기법인 EE(Elementary Effect)와 Embedded 기법인 RFR(Random Forest Regressor)을 비교한다.

EE 방법은 RFR보다 적은 평가 횟수로 정확도를 확보할 수 있다. RFR은 변수 선택을 위해 모델 자체의 정확도가 높아야 하지만, 빅데이터처럼 이미 생성된 데이터셋에는 더 적합하다. RFR의 공정한 비교를 위해 Autoencoder(AE)와도 성능을 시험했다. AE는 변수추출법으로서 적절한 변수 개수를 알기 어렵고, ANN 기반이라 하이퍼파라미터가 많아 구성이 어렵다는 단점이 있다. 결론적으로 RFR이 비교적 쉽게 더 나은 성능을 얻을 수 있는 사용자 친화적인 방법임을 확인했다.

서론​

최적설계에서 응답 예측은 매우 중요하며, 고려할 변수가 많아지면서 모델 정확도 확보와 전산 비용 감축을 위해 주요 인자(변수)를 판별하는 과정이 필요하다. 전통적으로 실험계획법(DOE)을 통한 통계적 해석(ANOVA 등)이 사용되었으나, 이후 전역민감도분석(GSA) 기법, 특히 Morris의 Elementary Effect(EE) 방법이 효율적인 대안으로 등장했다. 하지만 이러한 기법들은 원하는 방향으로 데이터를 생성해야 하므로, 무작위로 쌓인 빅데이터 처리에 한계가 있다. 이 한계를 극복하기 위해 Random Forest Regressor(RFR) 같은 모델 기반 차원축소 기법이 개발되었다. 본 논문은 서로 다른 배경에서 개발된 EE 기법과 RFR 기법을 비교 분석하는 것을 목적으로 한다.

배경​

차원축소(DR)는 크게 **변수선택(Feature Selection)**과 **변수추출(Feature Extraction)**로 나뉜다 (논문의 Figure 2.1 참조).

  1. 변수추출: 기존 변수의 조합으로 새로운 변수를 생성 (예: PCA, LDA, Autoencoder).
  2. 변수선택: 기존 변수 중 가장 영향력 있는 부분집합을 탐색하며, 3가지로 분류됨.
    • Filter: 모델 생성 없이 데이터의 통계적 특성(상관관계 등)으로 변수 순위를 매김 (GSA, EE 포함).
    • Wrapper: 모델의 성능(정확도)을 최대화하는 변수 부분집합을 탐색 (예: SFS, SBS). 계산 비용이 높음.
    • Embedded: 모델 훈련 과정에서 자연스럽게 변수 중요도를 계산 (예: LASSO, Ridge, RFR).

모델 아키텍처 / 방법론​

1. Elementary Effects (EE) Method​

Morris가 제안한 GSA 기법으로, 적은 실험 횟수로 변수의 선형성, 비선형성, 상호작용을 감지한다. 각 변수 XiX_i에 대해 p-수준 그리드에서 Δ\Delta만큼 이동 시 응답 YY의 변화를 계산한다.

  • 핵심 수식 (EE): EE=[Y(X1,...,Xi+Δ,...,Xk)−Y(X1,...,Xk)]ΔEE = \frac{[Y(X_1, ..., X_i+\Delta, ..., X_k) - Y(X_1, ..., X_k)]}{\Delta}
  • 민감도 지표: EE 분포의 절대값 평균(μ∗\mu^*)과 표준편차(σ\sigma)를 사용한다. μ∗\mu^*는 전반적 영향력, σ\sigma는 비선형성 및 상호작용을 나타낸다.
  • 알고리즘: 효율적 샘플링을 위해 'Trajectory sampling'을 사용하며(총 해석 수: r(k+1)r(k+1)), Campolongo의 Optimized Trajectory(OT)와 Khare의 Sampling for Uniformity(SU) 등이 비교 대상이다.

2. Random Forest Regressor (RFR)​

의사결정나무(DTR)의 앙상블 기법이다. DTR은 오버피팅에 취약하나, RFR은 부트스트랩(Bootstrap) 샘플링으로 k개의 DTR(약한 학습기)을 훈련시킨 후 예측값의 평균을 취해 오버피팅을 방지한다.

  • 핵심 구조 (Feature Importance, FI): RFR은 Embedded 방법으로, 훈련 과정에서 변수 중요도를 계산한다.
  • 알고리즘: 각 노드가 분기될 때 기준(MSE 또는 MAE)의 변화량을 측정하여 FI를 계산한다. (수식 4.2 참조: Feature Importance=Change in the criterion due to its nodesnumber of decision nodesFeature\ Importance = \frac{Change\ in\ the\ criterion\ due\ to\ its\ nodes}{number\ of\ decision\ nodes})
  • 응답에 영향이 없는 변수는 노드 생성에 기여하지 않아 FI가 0에 가까워진다.

실험 결과​

Test 1: EE vs. RFR (시뮬레이션)​

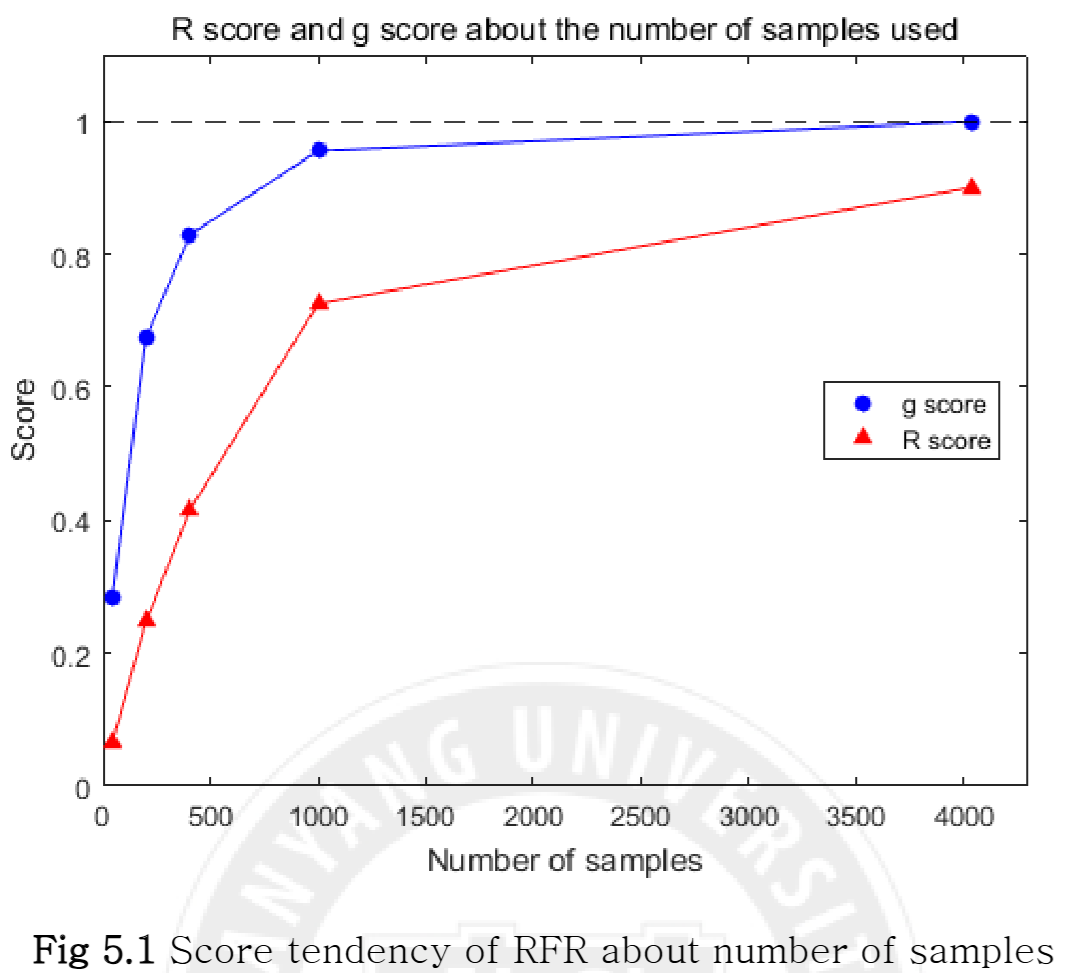
4가지 수학 함수(선형, G-function 등)를 사용해 비교했다.

  • EE 기법은 매우 적은 샘플 수(예: 44개)로도 높은 변수 선별 정확도를 달성했다.
  • EE 기법 중 Khare의 SU가 Campolongo의 OT보다 월등히 우수한 성능을 보였다 (Table 5.1). 이는 샘플링의 '균등성(Uniformity)' 확보가 중요함을 시사한다.
  • RFR은 EE보다 많은 샘플이 필요했으나(Fig 5.1), 샘플 수가 증가하면 정확도가 빠르게 향상되었다.
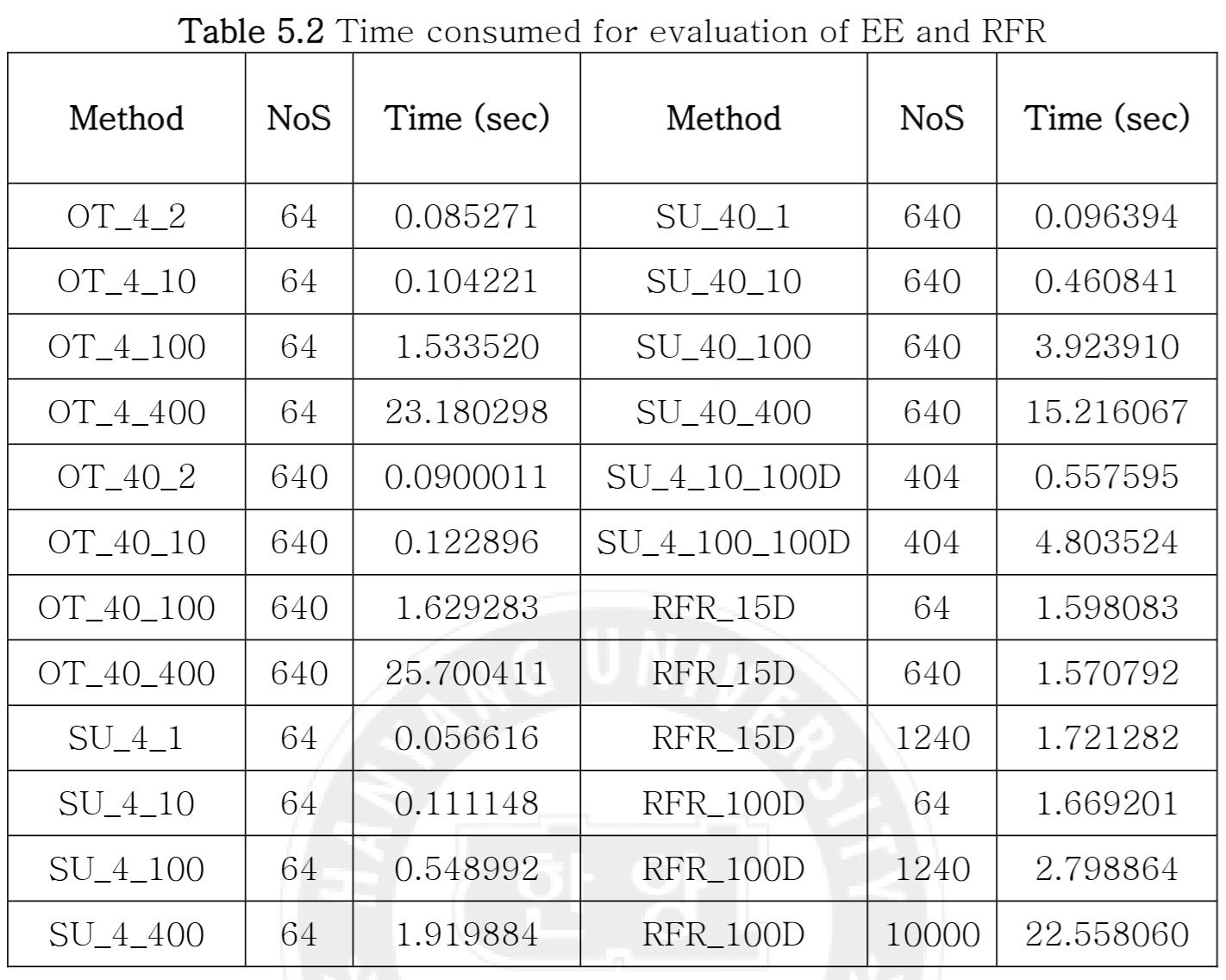
  • 시간 비용 면에서, SU는 OT보다 궤도 최적화(오버샘플링) 비용이 적어 효율적이었다 (Table 5.2).
  • 결론: 시뮬레이션 모델(데이터 생성 비용 높음)에서는 **EE (특히 SU 기법)**가 우수했다.

Test 2: RFR vs. Autoencoder (기존 데이터)​

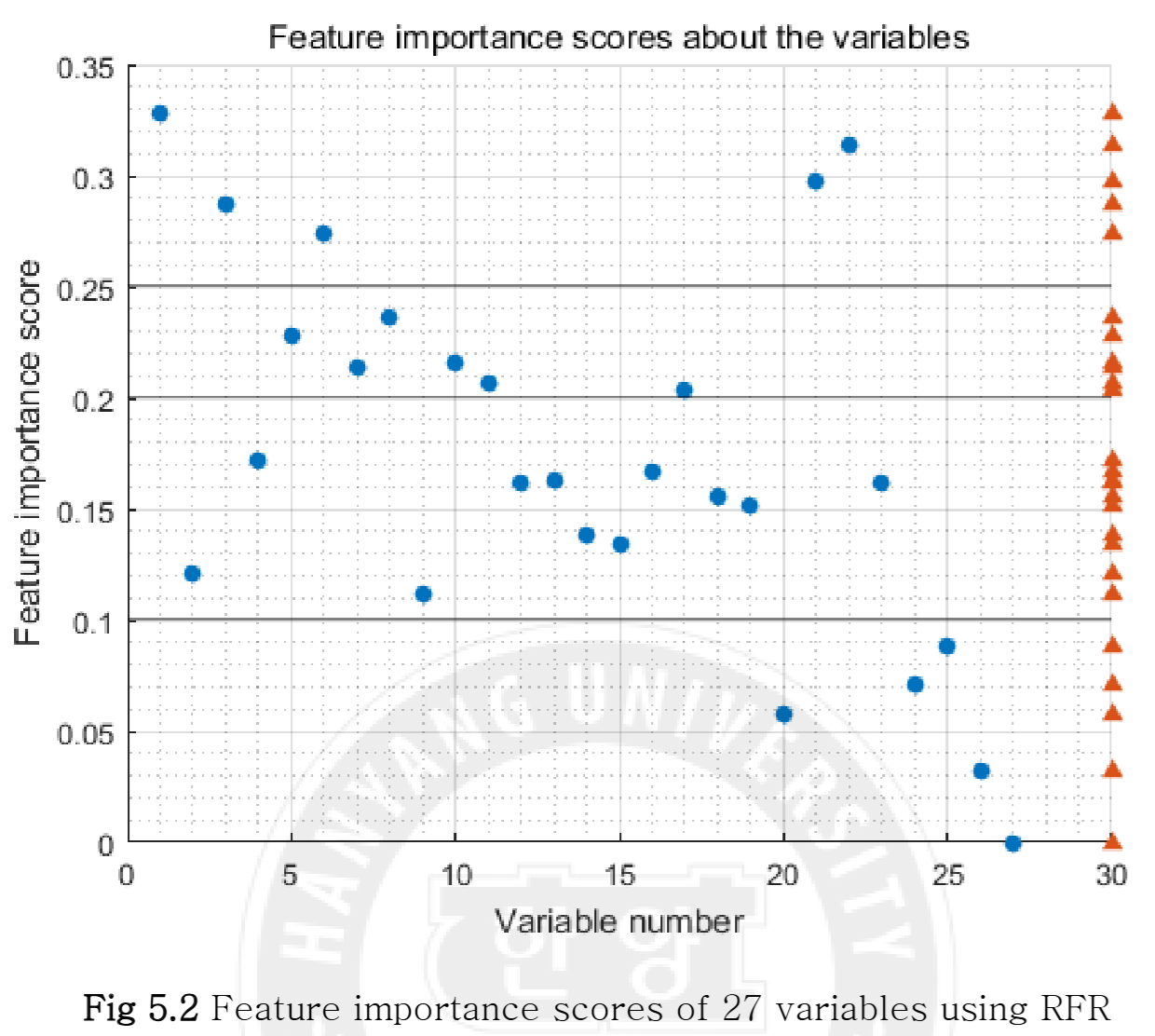
RFR은 기존 데이터 처리에 적합하므로, 변수추출 기법인 Autoencoder(AE)와 공정한 비교를 수행했다. (UCI 'Appliance energy prediction' 데이터, 27개 변수 사용)

  • RFR의 FI(Fig 5.2)를 사용해 변수를 3그룹(5개, 11개, 22개)으로 선택했다.
  • RFR은 영향력이 미흡한 5개 변수를 제거했을 때(RFR_3), 오히려 전체 변수를 사용했을 때보다 RMSE가 향상되었다(89.6 → 88.4). (Table 5.3)
  • AE로 동일 개수(5, 11, 22개)의 변수를 추출하여 RFR로 훈련시킨 결과, 모든 경우에서 변수 '선택'(RFR)을 사용했을 때보다 성능이 낮았다 (RMSE 증가). (Table 5.4)
  • 결론: RFR이 AE보다 사용이 편리하고(FI로 직관적 선택 가능) 성능도 우수했다.

결론​

차원축소 기법은 데이터 상황에 맞게 선택해야 한다.

  1. 시뮬레이션 (데이터 생성 필요): 적은 실험점으로 고차원 민감도 해석이 가능한 **EE (특히 SU 기법)**가 효율적이다.
  2. 기존 데이터 (빅데이터): RFR이 모델 정확도와 변수 중요도를 동시에 제공하며, 변수추출 기법인 Autoencoder보다 사용이 편리하고 좋은 성능을 보인다.
  3. Autoencoder는 적절한 변수 개수 설정이 어렵고, ANN 특유의 복잡한 하이퍼파라미터 튜닝이 필요해 성능 확보가 어렵다는 한계를 보였다.