WHAT DOES IT MEAN TO BE A TRANSFORMER? INSIGHTS FROM A THEORETICAL HESSIAN ANALYSIS

논문 정보

• 제목: WHAT DOES IT MEAN TO BE A TRANSFORMER? INSIGHTS FROM A THEORETICAL HESSIAN ANALYSIS
• 저자: Weronika Ormaniec (ETH Zürich), Felix Dangel (Vector Institute), Sidak Pal Singh (ETH Zürich)
• 학회/저널: ICLR 2025
• 발행일: 2025-03-17
• DOI: 해당 없음
• 주요 연구 내용: 단일 셀프 어텐션 레이어의 손실 함수에 대한 헤시안 행렬을 이론적으로 완전히 유도하고, 이를 행렬 미분 형태로 표현함. 헤시안의 각 블록이 데이터, 가중치, 어텐션 모멘트(attention moments)에 어떻게 의존하는지 분석하여 기존 MLP나 CNN과의 구조적 차이점을 명확히 함.
• 주요 결과 및 결론: 트랜스포머 헤시안은 파라미터 그룹(Query, Key, Value)에 따라 데이터와 가중치에 대한 의존성이 매우 비선형적이고 이질적(heterogeneous)임을 보임. Softmax 활성화 함수와 Query-Key 파라미터화와 같은 트랜스포머의 핵심 설계 요소가 이러한 이질성의 주요 원인임을 밝힘.
• 기여점: 트랜스포머 학습에 통용되는 적응형 옵티마이저, 레이어 정규화, 학습률 워밍업 등의 기법이 필요한 이유를 헤시안의 복잡하고 이질적인 구조를 통해 설명함. 이는 트랜스포머의 독특한 최적화 환경과 그로 인한 문제들에 대한 깊은 이론적 토대를 제공함.

요약

초록

트랜스포머 아키텍처는 딥러닝에 혁명을 일으켰지만, 왜 MLP나 CNN과 다른 최적화 기법들이 필요한지에 대한 근본적인 이유는 잘 알려져 있지 않다. 이 연구는 손실 함수의 헤시안(Hessian)을 이론적으로 비교 분석하여 트랜스포머와 다른 아키텍처의 근본적인 차이를 규명한다. 단일 셀프 어텐션 레이어에 대해 헤시안을 완전히 유도하고, 데이터, 가중치, 어텐션 모멘트에 대한 의존성을 분석하여 기존 네트워크와의 구조적 차이를 강조한다. 연구 결과, 트랜스포머에서 흔히 사용되는 아키텍처 및 최적화 선택들이 파라미터에 따라 매우 이질적으로 나타나는 데이터와 가중치에 대한 고도의 비선형적 의존성에 기인함을 시사한다.

서론

트랜스포머는 데이터가 셀프 어텐션 메커니즘을 통해 여러 번 입력되고, 내부적으로 Softmax 비선형성을 사용하며, Query와 Key 가중치 행렬이 직접 곱해지는 등 고유한 구조를 가진다. 이로 인해 Adam과 같은 적응형 옵티마이저, Layer Normalization, 학습률 워밍업 등이 필수적으로 사용된다. 이 연구의 목표는 이러한 현상들이 트랜스포머가 만드는 특정 손실 지형(loss landscape geometry)에 의해 어떻게 유발되는지를 헤시안 행렬의 구조를 이론적으로 분석하여 명확히 밝히는 것이다.

배경

연구는 단일 셀프 어텐션 레이어 $F(X) = A(X)XW_V$를 분석하며, 여기서 $A(X) = \text{softmax}(XW_QW_K^T/\sqrt{d_K})$ 이다. 분석의 핵심 도구는 손실 함수의 2차 미분인 헤시안 행렬 $H$이다. 헤시안은 연쇄 법칙에 따라 두 부분으로 분해될 수 있는데, 이를 가우스-뉴턴 분해(Gauss-Newton decomposition)라 한다: $H = H_o + H_f$.

• $H_o$: Outer-product Hessian. 손실 함수의 2차 미분에 의존하며 양의 준정부호(positive-semidefinite) 행렬이다.
• $H_f$: Functional Hessian. 네트워크 함수의 2차 미분에 의존하며, indefinite할 수 있다.

이 연구는 $W_Q, W_K, W_V$ 파라미터에 대한 헤시안의 각 블록을 분석한다.

모델 아키텍처 / 방법론

• 핵심 구조/방법: 단일 셀프 어텐션 레이어와 제곱 손실(square loss)을 가정하고, 파라미터 $W_Q, W_K, W_V$에 대한 전체 헤시안 행렬의 각 블록을 정확한 수식으로 유도한다. (Theorems 3.1, 3.2)
• 주요 구성 요소: 헤시안은 $H_o$와 $H_f$로 분해되며, 각 구성 요소는 데이터 행렬 $X$, 가중치 행렬 $W_Q, W_K, W_V$, 그리고 어텐션 분포의 모멘트(moment)에 복잡하게 의존한다.
• 수식:
  • Value 블록 ($H_o$): MLP의 헤시안과 유사한 구조를 가지며, 1차 어텐션 모멘트 $M_1=AX$에 의존한다. $H_{o}(W_{V},W_{V}) = \frac{2}{Ld_{V}}M_{1}^{\top}M_{1}\otimes I_{d_{V}}$
  • Query 블록 ($H_o$): $W_V, W_K$ 가중치와 데이터 $X$에 복잡하게 의존한다. $H_{o}(W_{Q},W_{Q}) = \frac{2}{Ld_{V}d_{K}}(I_{d_{V}}\otimes W_{K}^{\top})Z_{1}^{\top}(I_{L}\otimes W_{V}W_{V}^{\top})Z_{1}(I_{d_{V}}\otimes W_{K})$
  • Value 블록 ($H_f$): MLP와 유사하게 0이다. $H_{f}(W_{V},W_{V}) = 0$
  • 여기서 $Z_1$은 Softmax의 1차 미분과 데이터 $X$에 의존하는 항이다.
• 알고리즘: 유도된 헤시안 수식을 데이터 의존성, 어텐션 모멘트 의존성, 가중치 의존성의 세 가지 관점에서 분석한다. 또한 Softmax나 Query-Key 파라미터화를 제거한 변형 모델과의 비교를 통해 각 요소의 영향을 분석한다.

실험 결과

• 주요 데이터셋: GPT-2 단일 블록을 사용하여 숫자 덧셈을 다음 토큰 예측 문제로 변환한 데이터셋으로 실험을 진행했다.
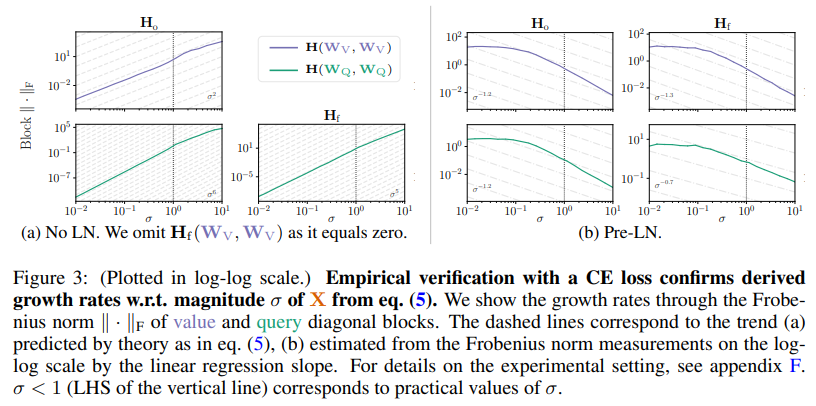
• 핵심 성능 지표: 헤시안 블록의 데이터 의존성이 파라미터 그룹별로 매우 이질적임을 발견했다. 예를 들어, $H_o$에서 Value 블록은 데이터 $X$의 크기에 제곱($\mathcal{O}(X^2)$)으로 비례하는 반면, Query/Key 블록은 6제곱($\mathcal{O}(X^6)$)에 비례한다. 이는 논문의 Figure 3a에서 입력 데이터의 표준편차 $\sigma$에 따른 헤시안 블록의 프로베니우스 노름(Frobenius norm) 변화를 통해 실험적으로 검증되었다.
• 비교 결과:
  • Layer Normalization: Pre-LN은 이러한 블록 간 데이터 의존성의 이질성을 완화하는 효과가 있음을 실험적으로 보였다 (논문의 Figure 3b).
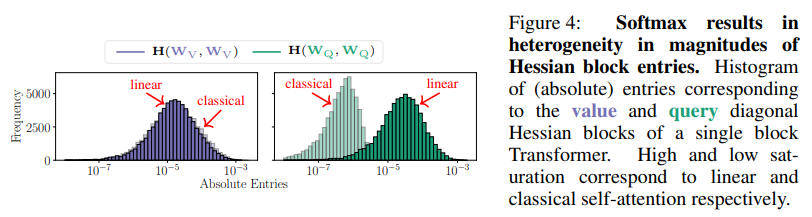
  • Softmax의 영향: Softmax를 제거하고 선형(linear) 어텐션으로 바꾸면 헤시안 블록들의 크기가 훨씬 균일해진다. 이는 논문의 Figure 4에서 히스토그램 비교를 통해 나타나며, Softmax가 헤시안의 이질성을 유발하는 주요 원인임을 시사한다. 또한 Softmax로 인해 $H_f$의 대각 블록이 0이 아니게 되어 헤시안이 더 indefinite(부정부호)해진다.
  • MLP와의 비교: 선형 셀프 어텐션을 깊게 쌓을 경우, 헤시안의 데이터 의존성은 층의 깊이 $D$에 따라 초지수적으로($\mathcal{O}(\Sigma_{XX}^{3^D})$) 증가한다. 이는 데이터 의존성이 깊이에 무관하게 일정($\mathcal{O}(\Sigma_{XX})$)한 선형 MLP와 극명한 대조를 이룬다.

결론

이 연구는 셀프 어텐션의 헤시안을 이론적으로 분석하여 트랜스포머의 독특한 최적화 특성을 규명했다. 헤시안의 각 블록이 데이터, 가중치, 어텐션 모멘트에 대해 매우 이질적이고 비선형적인 의존성을 갖는다는 것을 보였다. 이러한 이질성은 Softmax와 Query-Key 파라미터화 같은 트랜스포머의 핵심 설계에서 비롯되며, 이는 트랜스포머 학습이 왜 더 어렵고 적응형 옵티마이저나 레이어 정규화 같은 기법을 필요로 하는지에 대한 근본적인 설명을 제공한다. 이 연구는 향후 트랜스포머 맞춤형 최적화 알고리즘 개발을 위한 이론적 토대를 마련했다.