Generative Adversarial Nets

논문 정보

• 제목: Generative Adversarial Nets
• 저자: Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio (Université de Montréal)
• 학회/저널: arXiv preprint
• 발행일: 2014-06-10
• DOI: Not available in the provided text
• 주요 연구 내용: 생성 모델(Generator, G)과 판별 모델(Discriminator, D)을 동시에 학습시키는 적대적 과정(adversarial process) 프레임워크를 제안함. 생성자는 실제 데이터와 유사한 데이터를 생성하도록 학습하고, 판별자는 주어진 데이터가 실제인지 생성된 것인지 구별하도록 학습하며, 두 모델은 서로 경쟁하며 성능을 향상시킴.
• 주요 결과 및 결론: 제안된 프레임워크는 이론적으로 생성자가 실제 데이터 분포를 완벽하게 복제($p_g = p_{data}$)할 때 유일한 해가 존재함을 증명함. MNIST, TFD, CIFAR-10 데이터셋에 대한 실험을 통해 생성된 샘플의 질적, 양적 평가를 수행하여 프레임워크의 잠재력을 입증함.
• 기여점: 기존 생성 모델들의 주요 난관이었던 다루기 힘든 확률 계산(intractable probabilistic computations) 문제를 회피함. 역전파(backpropagation)만으로 전체 시스템을 학습할 수 있으며, 학습이나 샘플 생성 과정에서 마르코프 연쇄(Markov chains)가 필요 없는 새로운 생성 모델 학습 패러다임을 제시함.

요약

초록

생성 모델(G)과 판별 모델(D)이라는 두 모델을 동시에 학습시키는 새로운 적대적 과정 프레임워크를 제안한다. 생성자 G는 데이터 분포를 포착하여 실제와 같은 데이터를 생성하고, 판별자 D는 샘플이 학습 데이터에서 온 것인지 생성자 G가 만든 것인지 판별한다. 생성자 G의 학습 목표는 판별자 D가 실수를 저지를 확률을 최대화하는 것이다. 이 프레임워크는 두 플레이어가 참여하는 minimax 게임에 해당하며, G와 D가 충분한 용량(capacity)을 가질 때, G가 실제 데이터 분포를 복원하고 D는 모든 입력에 대해 1/2을 출력하는 유일한 해가 존재한다. 전체 시스템은 다층 퍼셉트론으로 구성될 경우 역전파만으로 학습이 가능하며, 학습 및 샘플 생성 과정에서 마르코프 연쇄나 근사 추론 네트워크가 필요 없다. 실험을 통해 생성된 샘플의 질적, 양적 평가를 진행하여 제안된 프레임워크의 잠재력을 입증했다.

서론

딥러닝 분야는 주로 판별 모델에서 큰 성공을 거두었으나, 생성 모델은 최대 가능도 추정(maximum likelihood estimation) 등에서 발생하는 다루기 힘든 확률 계산 문제로 인해 상대적으로 발전이 더뎠다. 이 논문은 이러한 어려움을 회피하는 새로운 생성 모델 추정 절차인 '적대적 신경망(adversarial nets)'을 제안한다. 이 프레임워크는 생성 모델과 판별 모델이라는 두 모델 간의 경쟁을 기반으로 한다. 생성 모델은 위조지폐범처럼 진짜와 구별하기 어려운 가짜 데이터를 생성하고, 판별 모델은 경찰처럼 진짜와 가짜를 구별하려고 시도한다. 이 경쟁 과정은 두 모델 모두의 성능을 향상시켜, 결국 생성된 가짜 데이터가 실제 데이터와 구별할 수 없는 수준에 이르게 한다.

배경

기존의 주요 딥 생성 모델로는 RBM, DBM과 같은 무방향 그래픽 모델과 DBN과 같은 하이브리드 모델이 있었다. 이 모델들은 분배 함수(partition function)와 그 기울기를 정확히 계산하기 어려워 MCMC(Markov chain Monte Carlo)와 같은 방법에 의존했지만, 이는 학습을 어렵게 만드는 주요 원인이었다. Score matching이나 Noise-contrastive estimation(NCE)과 같이 로그 가능도를 근사하지 않는 대안들도 제안되었으나, 이들은 학습된 확률 밀도가 정규화 상수를 제외하고 분석적으로 다루기 용이해야 한다는 한계가 있었다. 반면, GAN은 명시적인 확률 분포를 정의하지 않고 샘플을 생성하는 기계를 역전파를 통해 직접 학습시킨다는 점에서 차별화되며, GSN과 달리 샘플링 과정에서 마르코프 연쇄가 필요 없다.

모델 아키텍처 / 방법론

• 핵심 구조/방법: 적대적 네트워크는 두 개의 다층 퍼셉트론(MLP), 즉 생성자(Generator, G)와 판별자(Discriminator, D)로 구성된다. 생성자 G는 노이즈 변수 $z$에 대한 사전분포 $p_z(z)$로부터 샘플링된 노이즈를 입력받아 데이터 공간으로 매핑하는 미분 가능한 함수 $G(z; \theta_g)$이다. 판별자 D는 입력 데이터 $x$가 실제 데이터 분포 $p_{data}$에서 왔을 확률을 나타내는 단일 스칼라 값 $D(x; \theta_d)$를 출력한다.

• 주요 구성 요소:

  • 생성자 (Generator, G): 랜덤 노이즈 $z$로부터 가짜 데이터 샘플 $G(z)$를 생성한다.
  • 판별자 (Discriminator, D): 실제 데이터 $x$와 생성자가 만든 가짜 데이터 $G(z)$를 구별한다. $D(x)$의 출력값은 1(실제) 또는 0(가짜)에 가까워지도록 학습된다.

• 수식: D와 G는 다음의 가치 함수 $V(D, G)$에 대한 2인 minimax game을 통해 학습된다. D는 이 값을 최대화하려 하고, G는 최소화하려고 한다. $min_G max_D V(D,G) = \mathbb{E}_{x \sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$ 이론적으로 이 게임의 최적점은 $p_g = p_{data}$이며, 이때 판별자는 어떤 입력에 대해서도 진짜와 가짜를 구별할 수 없게 되어 $D(x) = \frac{1}{2}$이 된다.

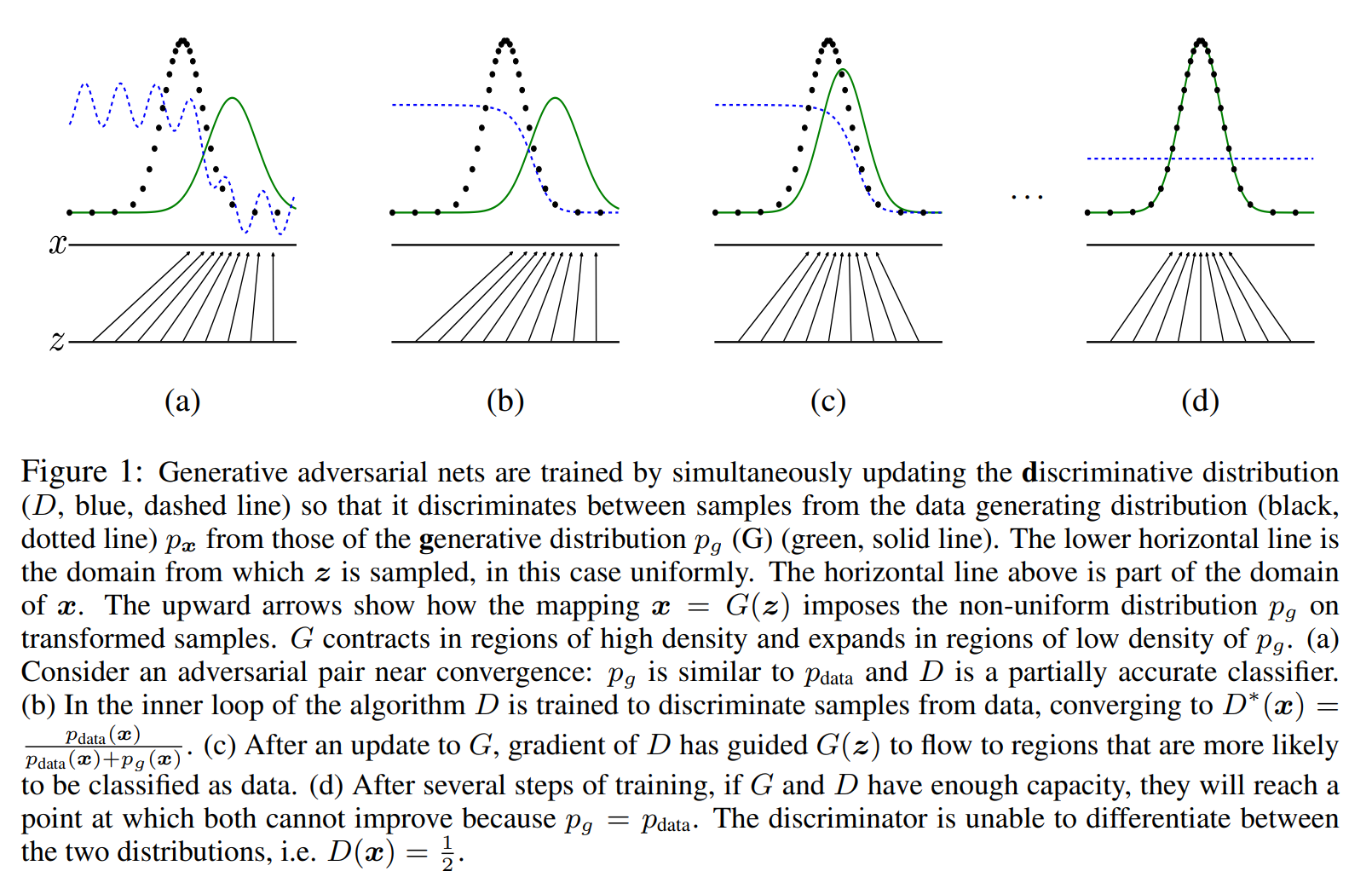
• 알고리즘: 학습은 판별자 D를 k 스텝 최적화하고 생성자 G를 1 스텝 최적화하는 과정을 반복하여 진행된다(실험에서는 k=1을 사용). D는 확률적 경사 상승법으로, G는 확률적 경사 하강법으로 업데이트된다. 학습 초기에 $log(1 - D(G(z)))$의 그래디언트가 사라지는 문제를 완화하기 위해, G가 $log(D(G(z)))$를 최대화하도록 학습 목표를 변경할 수 있다. 논문의 Figure 1은 이 적대적 학습 과정을 시각적으로 보여준다.

실험 결과

• 주요 데이터셋: MNIST, Toronto Face Database(TFD), CIFAR-10 데이터셋을 사용하여 모델의 성능을 평가했다. 생성자는 ReLU와 시그모이드 활성화 함수를 혼합하여 사용했고, 판별자는 Maxout 활성화 함수를 사용했다.

• 핵심 성능 지표: 생성된 샘플에 가우시안 파젠 윈도우(Gaussian Parzen window)를 적용하여 테스트 데이터셋에 대한 로그 가능도(log-likelihood)를 추정하는 방식으로 정량 평가를 수행했다.

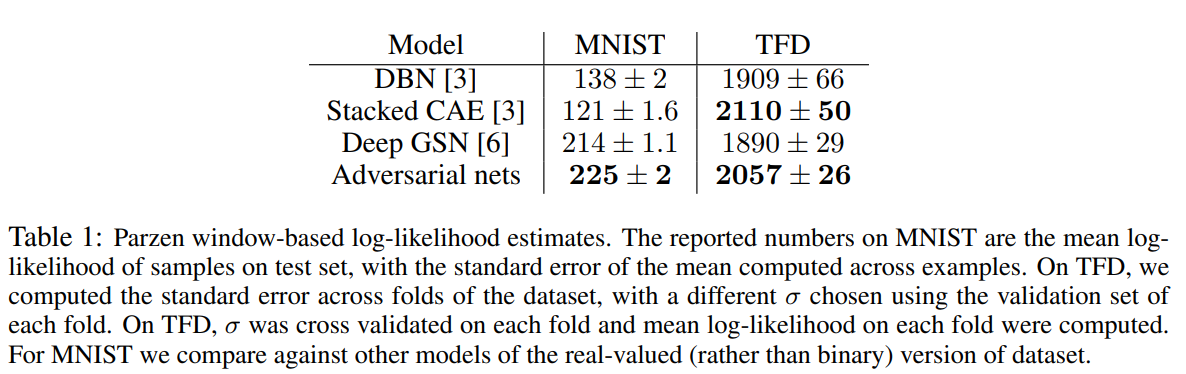
• 비교 결과: Table 1 에 제시된 결과에 따르면, Adversarial nets는 MNIST에서 225 ± 2, TFD에서 2057 ± 26의 평균 로그 가능도를 기록했다. 이는 DBN, Stacked CAE 등 당시의 다른 생성 모델들과 비교했을 때 경쟁력 있는 성능이다. 논문의 Figure 2 는 각 데이터셋에 대해 생성된 이미지 샘플들을 보여주는데, 이 샘플들은 훈련 데이터를 단순히 암기한 것이 아니며, 기존의 우수한 생성 모델들과 비교해도 뒤지지 않는 품질을 보여준다.

결론

이 연구는 적대적 모델링 프레임워크의 성공적인 가능성을 입증했다. GAN의 주요 장점은 다음과 같다. 첫째, 마르코프 연쇄가 필요 없고 역전파만으로 모든 그래디언트를 계산할 수 있다. 둘째, 학습 과정에서 별도의 추론이 필요 없으며, 다양한 미분 가능한 함수를 생성자와 판별자에 사용할 수 있어 설계가 유연하다. 또한, 생성자가 실제 데이터 예시를 직접 보지 않고 판별자를 통해 전달된 그래디언트로만 학습하기 때문에 통계적 이점을 가질 수 있으며, 매우 날카로운(sharp) 분포도 모델링할 수 있다. 향후 연구 방향으로는 조건부 생성 모델($p(x|c)$)로의 확장, 준지도 학습(semi-supervised learning)에의 활용, 그리고 G와 D의 학습을 안정화하고 효율을 높이는 방법론 개발 등이 있다.