소프트웨어공학특론
손정주 교수님
시험 준비
1. Prioritise tests to maximise early unique line coverage.
Coverage Matrix:
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| T1 | 1 | 1 | 0 | 0 | 0 |
| T2 | 0 | 1 | 1 | 0 | 0 |
| T3 | 0 | 0 | 1 | 1 | 0 |
| T4 | 1 | 0 | 0 | 1 | 1 |
- Tasks:
- A. Define the Representation of a GA individual.
- B. Define a fitness that rewards earlier unique coverage(earlier in a "collective" sense)
- C. Give one crossover and one mutation operator for your representation.
- D. With population size=2, parents Compute each order's coverage progression and your fitness. Create two plausible offspring and estimate their fitness.
- E. Pcik the next generation (size=2) under: i)elitism, ii) generational replacement, iii) gradual replacement (top k). State the average fitness for each.
Answer
GA를 이용한 Early unique line coverage를 최대화하는 테스트 실행 순서 찾는 문제 데이터:
- Statements: {S1, S2, S3, S4, S5}
- T1: {S1, S2}
- T2: {S2, S3}
- T3: {S3, S4}
- T4: {S1, S4, S5} A. GA 개체(Individual)의 표현
- 해석: GA가 탐색할 해(solution)를 유전형(genotype)으로 어떻게 표현할지 정의하는 문제
- 풀이: 이 문제는 테스트 케이스 T1, T2, T3, T4의 순서를 찾는 문제 개체(individual)는 테스트 케이스의 순열(permutation)로 표현 가능 - 예시: 또는 B. 적합도(Fitness) 함수
- 해석: 초기에 고유한 커버리지를 달성하는 순서에 높은 점수를 주는 적합도 함수 정의 문제
- 풀이: 4번 문제에서 정의된 조기 커버리지 점수(Early coverage score) 5를 사용 이 점수는 각 테스트 실행 후 누적된 고유 라인 커버리지 비율의 평균 - 계산식: - : 총 테스트 케이스 수 (여기서는 4) - : 번째 테스트까지 실행했을 때의 누적 고유 라인 커버리지 비율 ( (누적 고유 라인 수) / (총 고유 라인 수 5) ) - 이 점수가 높을수록 초반에 더 많은 라인을 커버한다는 의미 C. 교배(Crossover) 및 돌연변이(Mutation) 연산자
- 해석: A에서 정의한 순열 표현에 적합한 교배 연산자 1개와 돌연변이 연산자 1개를 제시하는 문제
- 풀이: - 교배 (Crossover): 순서 기반 표현이므로 순서 교배(Order Crossover, OX) 또는 부분 매핑 교배(Partially Mapped Crossover, PMX)를 사용 가능 - 돌연변이 (Mutation): 교환 돌연변이(Swap Mutation)를 사용 가능 (예: 순열에서 임의의 두 테스트 위치를 서로 맞바꿈. ) D. 부모 및 자손 적합도 계산
- 부모 =
- T1: {S1, S2}. 누적: {S1, S2}. (2/5 = 0.4)
- T2: {S2, S3}. 누적: {S1, S2, S3}. (3/5 = 0.6)
- T3: {S3, S4}. 누적: {S1, S2, S3, S4}. (4/5 = 0.8)
- T4: {S1, S4, S5}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- 적합도:
- 부모 =
- T4: {S1, S4, S5}. 누적: {S1, S4, S5}. (3/5 = 0.6)
- T3: {S3, S4}. 누적: {S1, S3, S4, S5}. (4/5 = 0.8)
- T2: {S2, S3}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- T1: {S1, S2}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- 적합도:
- 그럴듯한 자손 2개 생성 및 적합도 추정 - 자손 1 (): 에 Swap(T2, T4) 돌연변이 적용 - 1. T1: {S1, S2}. 누적: {S1, S2}. (2/5 = 0.4) 2. T4: {S1, S4, S5}. 누적: {S1, S2, S4, S5}. (4/5 = 0.8) 3. T3: {S3, S4}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0) 4. T2: {S2, S3}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0) - 적합도: - 자손 2 (): 에 Swap(T3, T2) 돌연변이 적용 - 1. T4: {S1, S4, S5}. 누적: {S1, S4, S5}. (3/5 = 0.6) 2. T2: {S2, S3}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0) 3. T3: {S3, S4}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0) 4. T1: {S1, S2}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0) - 적합도: E. 다음 세대 선정 (크기=2)
- 현재 풀(Pool): , , ,
- 적합도 순위:
- i) 엘리트주의 (Elitism):
- 방식: 부모와 자손을 합친 전체 풀에서 적합도가 가장 높은 2개를 선택
- 다음 세대: { , }
- 평균 적합도:
- ii) 세대 교체 (Generational replacement):
- 방식: 부모 세대()를 자손 세대()로 완전히 교체
- 다음 세대: { , }
- 평균 적합도:
- iii) 점진적 교체 (Gradual replacement, top k):
- 방식: "top k" 12는 보통 전체 풀에서 상위 k개(여기서는 k=2)를 선택하는 것을 의미하며, 이는 (i) 엘리트주의와 동일
- 다음 세대: { , }
- 평균 적합도:
2. APR via GA
GA를 이용한 자동 프로그램 수정(APR) 문제.
Buggy code:
def shipping_fee(weight_kg):
# policy: fee is 0 when weight $\le5$, otherwise 10
if weight_kg < 5: #faulty operator; should be <=
return 0
else:
return 10
Test suite (oracle):
- T1:
shipping_fee(0) → 0 - T2:
shipping_fee(5) → 0 - T3:
shipping_fee(5.0) → 0 - T4:
shipping_fee(6) → 10
A. Define a genotype with a minimal set of editable choices, and explain how it maps to the phenotype (the concrete program).
- 해석: 버그 수정을 위한 "최소한의 편집 선택"을 유전형(genotype)으로 정의하고, 이것이 실제 코드(phenotype)로 어떻게 매핑되는지 설명하는 문제.
- 풀이:
- 유전형 (Genotype): 버그가 있는 18번 라인의 비교 연산자 (
<)를 대체할 연산자를 나타내는 정수(Integer)이다. - 표현형 (Phenotype): 유전형에 따라 연산자가 수정된 실제 Python 코드이다.
- 매핑 (Mapping):
- 1
if weight_kg < 5: - 2
if weight_kg <= 5: - 3
if weight_kg > 5: - 4
if weight_kg >= 5: - 5
if weight_kg == 5: - 6
if weight_kg != 5:
- 1
- 유전형 (Genotype): 버그가 있는 18번 라인의 비교 연산자 (
B. Specify one mutation operator and (if applicable) one crossover operator for your representation.
- 해석: A에서 정의한 표현형에 맞는 돌연변이 연산자 1개와 (적용 가능하다면) 교배 연산자 1개를 지정하는 문제.
- 풀이:
- 돌연변이 (Mutation): 무작위 리셋(Random Resetting). 현재 유전형(예: 1)을 다른 가능한 정수(예: 2~6 중 하나)로 무작위 변경한다.
- 교배 (Crossover): 이 유전형은 단일 유전자(정수 하나)로 구성되어 교배가 큰 의미가 없다. (만약 유전형이
[연산자, 값]처럼 여러 유전자로 구성되었다면, 균등 교배(Uniform Crossover)를 사용할 수 있다.)
C. Define a fitness based on the test suite above.
- 해석: 테스트 스위트를 기반으로 적합도를 정의하는 문제.
- 풀이: (통과한 테스트 케이스 수) / (전체 테스트 케이스 수)
- (여기서 Pass(T)는 통과 시 1, 실패 시 0이다.)
D. Compute fitness for these two candidate programs:
- 해석: (버그 버전)과 (패치 버전)의 적합도를 C에서 정의한 함수로 계산한다.
- 풀이:
- :
if weight_kg < 5:(버그 버전)- T1(0):
0 < 5(True) 0. (통과) - T2(5):
5 < 5(False) 10. (실패, 0 기대) - T3(5.0):
5.0 < 5(False) 10. (실패, 0 기대) - T4(6):
6 < 5(False) 10. (통과) - 적합도: (1 + 0 + 0 + 1) / 4 = 2 / 4 = 0.5
- T1(0):
- :
if weight_kg <= 5:(패치 버전)- T1(0):
0 <= 5(True) 0. (통과) - T2(5):
5 <= 5(True) 0. (통과) - T3(5.0):
5.0 <= 5(True) 0. (통과) - T4(6):
6 <= 5(False) 10. (통과) - 적합도: (1 + 1 + 1 + 1) / 4 = 4 / 4 = 1.0
- T1(0):
- :
E. If your population contains only and , which next-generation policy would you prefer and why?
- 해석: 현재 인구(population)가 (적합도 0.5)과 (적합도 1.0)만으로 구성될 때, 어떤 세대 교체 정책을 선호하는지 묻는 문제.
- 풀이:
- 선호 정책: 엘리트주의(Elitism) 또는 점진적 교체(Gradual replacement (top k))
- 이유: 현재 인구에 완벽한 해(적합도 1.0)인 가 이미 존재한다. 엘리트주의는 현 세대의 가장 우수한 개체를 다음 세대로 무조건 생존시키므로, 이 완벽한 해()를 잃어버릴 위험이 없다. 반면, 세대 교체(Generational replacement)는 모든 부모()를 자손으로 대체하는데, 이 과정에서 완벽한 해가 소실될 위험이 있다.
3. Coverage Computation
주어진 코드와 테스트 스위트에 대한 커버리지를 계산하는 문제.
def f(a, b, c):
if a and b: # D1
S2: $x=1$
else:
S3: $x=2$
if c: # D2
S5: $y=x+1$
else:
S6: $y=x-1$
S7: return y
Test suite:
- T1:
(a=True, b=False, c=True) - T2:
(a=True, b=True, c=False)
A. For T1 and T2, list the statements executed and compute overall statement coverage.
- 해석: T1과 T2가 실행하는 구문(S)을 나열하고, 전체 구문 커버리지를 계산한다.
- 풀이:
- T1 실행 구문:
if True and False:(False) else 실행- S3
if True:(True)- S5
- S7
- 실행된 구문: {S3, S5, S7}
- T2 실행 구문:
if True and True:(True)- S2
if False:(False) else 실행- S6
- S7
- 실행된 구문: {S2, S6, S7}
- 전체 구문 커버리지:
- 전체 구문: {S2, S3, S5, S6, S7} (총 5개)
- 실행된 구문: {S2, S3, S5, S6, S7} (5개 모두 실행)
- 커버리지: 5 / 5 = 100%
- T1 실행 구문:
B. Compute decision (branch) coverage for D1 and D2.
- 해석: D1(
a and b)과 D2(c)의 결정(분기) 커버리지를 계산한다. - 풀이:
- D1 (
if a and b):- T1:
a and b= False (Else 브랜치 커버) - T2:
a and b= True (If 브랜치 커버) - D1 커버리지: 2 / 2 = 100%
- T1:
- D2 (
if c):- T1:
c= True (If 브랜치 커버) - T2:
c= False (Else 브랜치 커버) - D2 커버리지: 2 / 2 = 100%
- T1:
- D1 (
C. Compute condition coverage for a, b, and c.
- 해석: 개별 조건 각각의 T/F 커버리지를 계산한다.
- 풀이:
- 전체 조건:
- 조건 'a':
- T1:
- T2:
- 결과: True만 커버, False는 커버 안 됨.
- 'a' 커버리지: 1 / 2 = 50%
- 조건 'b':
- T1:
- T2:
- 결과: True, False 모두 커버.
- 'b' 커버리지: 2 / 2 = 100%
- 조건 'c':
- T1:
- T2:
- 결과: True, False 모두 커버.
- 'c' 커버리지: 2 / 2 = 100%
D. Is the current test suite MC/DC-adequate for D1?
- 해석: D1 (
if a and b)에 대해 MC/DC가 충족되었는지 묻는 문제. MC/DC는 각 개별 조건(a, b)이 다른 조건은 고정한 채 자신(T/F)만 변경되어 전체 결정(D1)의 결과(T/F)를 바꾸는 테스트 쌍이 존재하는지를 본다. - 풀이: 아니다.
- 'b'에 대한 독립적 영향:
- T2: () D1 = True
- T1: () D1 = False
- 'a'가 True로 고정된 상태에서 'b'가 T/F로 바뀌자 D1이 T/F로 바뀌었다. ('b'는 MC/DC 만족)
- 'a'에 대한 독립적 영향:
- T2: () D1 = True
- (필요한 테스트): () D1 = False
- 'b'가 True로 고정된 상태에서 'a'가 T/F로 바뀌는 쌍이 필요하다. 하지만 현재 테스트 스위트에는 ()인 경우가 없다.
- 결론: 'a'에 대한 MC/DC 쌍이 없으므로 D1은 MC/DC를 충족하지 못한다.
- 'b'에 대한 독립적 영향:
4. Coverage and Fault Detection
두 가지 테스트 순서 와 를 '조기 커버리지 점수'와 'APFD' (여기서는 APFD'로 정의됨) 관점에서 비교하는 문제.
Coverage Matrix (S1-S5, 총 5개):
- T1: {S1, S2}
- T2: {S2, S3}
- T3: {S3, S4}
- T4: {S1, S4, S5}
Fault Detection Matrix (F1-F2, 총 2개):
- T1: {}
- T2: {F1}
- T3: {F2}
- T4: {}
A. For compute the cumulative unique coverage after each position and the early coverage score. Do the same for .
- 해석: 와 각각에 대해 "각 테스트 실행 후 누적된 고유 라인 커버리지 비율의 평균" (조기 커버리지 점수)을 계산한다.
- 풀이:
- 순서 : [T4, T1, T2, T3]
- T4: {S1, S4, S5}. 누적: {S1, S4, S5}. (3/5 = 0.6)
- T1: {S1, S2}. 누적: {S1, S2, S4, S5}. (4/5 = 0.8)
- T2: {S2, S3}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- T3: {S3, S4}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- 조기 커버리지 점수: $(0.6 + 0.8 + 1.0 + 1.0) / 4 = 3.4 / 4 = 0.85
- 순서 : [T2, T3, T4, T1]
- T2: {S2, S3}. 누적: {S2, S3}. (2/5 = 0.4)
- T3: {S3, S4}. 누적: {S2, S3, S4}. (3/5 = 0.6)
- T4: {S1, S4, S5}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- T1: {S1, S2}. 누적: {S1, S2, S3, S4, S5}. (5/5 = 1.0)
- 조기 커버리지 점수: $(0.4 + 0.6 + 1.0 + 1.0) / 4 = 3.0 / 4 = 0.75
- 순서 : [T4, T1, T2, T3]
B. For compute the cumulative unique faults detected after each position and APFD'. Do the same for .
- 해석: 와 각각에 대해 "각 테스트 실행 후 누적된 고유 결함 탐지 비율의 평균" (APFD')을 계산한다.
- 풀이:
- 순서 : [T4, T1, T2, T3]
- T4: {}. 누적: {}. (0/2 = 0.0)
- T1: {}. 누적: {}. (0/2 = 0.0)
- T2: {F1}. 누적: {F1}. (1/2 = 0.5)
- T3: {F2}. 누적: {F1, F2}. (2/2 = 1.0)
- APFD': $(0.0 + 0.0 + 0.5 + 1.0) / 4 = 1.5 / 4 = 0.375
- 순서 : [T2, T3, T4, T1]
- T2: {F1}. 누적: {F1}. (1/2 = 0.5)
- T3: {F2}. 누적: {F1, F2}. (2/2 = 1.0)
- T4: {}. 누적: {F1, F2}. (2/2 = 1.0)
- T1: {}. 누적: {F1, F2}. (2/2 = 1.0)
- APFD': $(0.5 + 1.0 + 1.0 + 1.0) / 4 = 3.5 / 4 = 0.875
- 순서 : [T4, T1, T2, T3]
C. Which order is better for coverage? Which is better for fault detection?
- 해석: A와 B의 계산 결과를 비교한다.
- 풀이:
- 커버리지:
- 결함 탐지:
- 결론:
- 커버리지 측면에서는 가 더 좋다.
- 결함 탐지 측면에서는 가 더 좋다.
Intro
1. 기본 정보
- 과목명: Advanced Software Engineering
- 과목 코드: COMP0730-001
- 담당 교수: 손정주 교수님(Jeongju Sohn)
- 소속: 경북대학교 컴퓨터학부
- 교수 이메일: jeongju.sohn@knu.ac.kr
- 교수 연구실: IT5-207
- 평가 비율
- 출석: 10%
- 과제 (논문 리뷰): 15%
- 중간고사: 35% 10
- 기말 (연구 제안서): 30% 11
- 발표 (논문 발표): 10% 12
3. 교재 정보
- 주 교재: Software Engineering, 10th Edition (Ian Sommerville 저)
- 부 교재: Software Engineering at Google (Titus Winters 등 저)
- 참고: 수업은 주로 강의 슬라이드, 자료 및 최신 연구 논문을 기반으로 진행될 예정
4. 평가 항목 상세
출석 (10%)
- LMS를 통해 수업 중 출석 체크 진행
- 수업의 이상 결석 시 자동으로 F 학점 처리 과제 (15%) 19
- 총 2편의 논문 리뷰를 수행
- 실제 리뷰어처럼 비판적(Offensive X, Critical O)으로 강점과 약점을 포함하여 리뷰
- 개인 리뷰 (1편): 학생이 직접 선택한 논문 1편을 리뷰.
- 그룹 리뷰 (1편): 3-4명으로 그룹을 구성하여 논문 1편 선정. 각자 개별 리뷰 작성 후, 토론을 통해 그룹의 최종 결정을 담은 '메타 리뷰'를 작성. 발표 (10%)
- 논문 리뷰 발표 (5%): 그룹 리뷰를 수행한 논문과 그룹의 (메타) 리뷰 및 결정 발표. 이후 수업 전체 토론(Class PC decision) 진행
- 연구 제안서 발표 (5%): 자신의 연구 아이디어에 대해 5분 (최대 10분)간 발표. 중간고사 (35%) 및 기말 (30%)
- 중간고사 (35%): 일반적인 중간고사 시험.
- 기말 (30%): 연구 제안서(Research Proposal) 작성.
- 주제: 자동화된 테스팅, 디버깅(결함 위치 파악, 자동 프로그램 수정 등), 결함 예측, AI를 위한 SE 등에서 선택하거나 자기가 선정한 분야 가능
- 포함 내용:
- 동기 (Motivation): 어떤 문제인지, 왜 중요한지
- 핵심 아이디어 및 아키텍처: 입력 -> 프로세스 -> 출력
- 기존 연구와의 차별성 (Novelty): 차이점, 해결하려는 격차
- (선택 사항) 평가 계획 (Evaluation plan)
5. 강의 개요 (Lec 1: Introduction)
- 소프트웨어 공학(SE)이란? 소프트웨어의 설계, 개발, 테스트 및 유지보수에 중점을 둔 공학 분야, 신뢰할 수 있는 시스템을 구축하기 위한 체계적인 원칙 기반 방법론을 다룸
- '공학'이 필요한 이유: 초기 소프트웨어는 체계적이지 않았으나, 시스템의 규모와 복잡성이 증가하며 비용 초과, 신뢰성 문제 등 '소프트웨어 위기(Software Crisis)'가 대두됨.
- 물리적 시스템과의 차이: 소프트웨어는 무형적(intangible)이고, 복잡성이 높으며(high complexity), 잦은 변경(frequent changes)이 발생.
- 소프트웨어 공학의 본질적 어려움: 'No Silver Bullet'에서 언급된 것처럼, 소프트웨어는 본질적으로 복잡성(Complexity), 순응성(Conformity), 변경성(Changeability), 비가시성(Invisibility)이라는 어려움을 가지며, 모든 것을 해결할 만능 해결책(silver-bullet)은 없다.
- 자동화(Automation) 및 최적화(Optimisation)의 필요성: 현대 소프트웨어는 규모가 방대하고(수백만 LOC), 인간의 수동 작업은 비용이 많이 들고 오류가 발생하기 쉬움. 따라서 SE는 개발 및 유지보수 규모를 확장할 수 있는 프로세스와 도구에 관한 것이며, 이 과정에서 자동화와 최적화가 필수적.
6. 잠정 강의 일정 (Tentative Schedule)
- Intro (Done!)
- 메타휴리스틱 (Metaheuristics) (Done!)
- 진화 연산 (Evolutionary Computation) (Done!)
- 검색 기반 소프트웨어 공학의 기초 (Foundations of Search-Based Software Engineering) (Done!)
- 자동화된 소프트웨어 테스팅 (Automated Software Testing) (Done!)
- 뮤테이션 테스팅 및 테스트 품질 평가 (Mutation Testing and Test Quality Assessment)
- 결함 위치 파악 (Fault Localisation)
- 중간고사
- 자동화된 프로그램 수정 (Automated Program Repair) (발표 + 강의)
- SE의 예측 모델 (Predictive Models in SE) (발표 + 강의)
- 코드의 자연스러움 (The Naturalness of Code) (발표 + 강의)
- LLM 기반 디버깅 및 설명 (LLM-based Debugging and Explanation) (발표 + 강의)
- 테스트 변덕성 및 영향 (Test Flakiness and Impact) (발표 + 강의)
- AI를 위한 소프트웨어 공학 (Software Engineering for AI) (발표 + 강의)
- 기말 (프로젝트 제안서) (Final Term (Project Proposal))
Metaheuristic
1.메타휴리스틱 (Metaheuristics)의 정의
- 휴리스틱 (Heuristics): 특정 문제를 해결할 때 사용하는 실용적인 접근 방식이나 '지름길'을 의미한다. 이 방법은 모든 경우에 최적의 해를 보장하지는 않지만(not fully optimised), 제한된 시간 내에 '그럭저럭 괜찮은(good enough)' 근사 해를 제공하는 것을 목표로 한다.
- 메타 (Meta): "넘어서(beyond)" 또는 "그 자체에 대한(about itself)"이라는 의미를 가진 접두사이다.
- 메타휴리스틱 (Metaheuristics): Heuristics의 상위 개념이다. 단일 문제에 국한된 Heuristics를 넘어, 다양한 유형의 문제에 적용될 수 있도록 Heuristics를 안내하고, 조정하며, 일반화하는 상위 레벨의 전략 프레임워크(high-level general framework)이다.
- 이는 본질적으로 "똑똑한 시행착오(Smart trial and error)" 전략으로 볼 수 있다. 무작위적인 시도가 아니라, 이전 시도의 결과를 바탕으로 더 나은 해를 찾도록 탐색 과정을 지능적으로 안내한다.
- 범용성: 특정 문제에 종속되지 않는다. 예를 들어, 8-Queens 문제나 자동 패치 생성 문제 모두에 동일한 Metaheuristics 알고리즘(예: 유전 알고리즘)을 적용할 수 있다.
- 근사적 및 비결정적: 최적의 해를 항상 보장하기보다는, 실용적인 시간 내에 만족스러운 수준의 해를 찾는 것을 목표로 한다.
- 근사적 (Approximate): 최적해가 아닌, 최적해에 가까운 해를 찾는다.
- 비결정적 (Non-deterministic): 알고리즘을 실행할 때마다 탐색 경로가 달라질 수 있으며, 결과적으로 다른 해를 찾을 수 있다 (예: 무작위 초기화, 확률적 연산자 사용).
2. 메타휴리스틱 (Metaheuristics)의 4가지 핵심 요소
모든 Metaheuristics 접근법을 설계하고 이해하기 위해서는 다음 4가지 핵심 요소를 정의해야 한다.
- 표현 (Representation):
- "무엇을 시도할 것인가?" 즉, 문제의 해(solution)를 컴퓨터가 처리할 수 있는 형태로 인코딩(encoding)하는 방식이다.
- 이 Representation이 검색 공간(search space)의 형태를 결정한다.
- 예: 8-Queens 문제는 8개 퀸의 위치 좌표 배열로 표현할 수 있다. 자동 패치 생성(APR) 문제는 코드에 적용할 변경 사항(edit)의 순열(sequence of edits)로 표현할 수 있다.
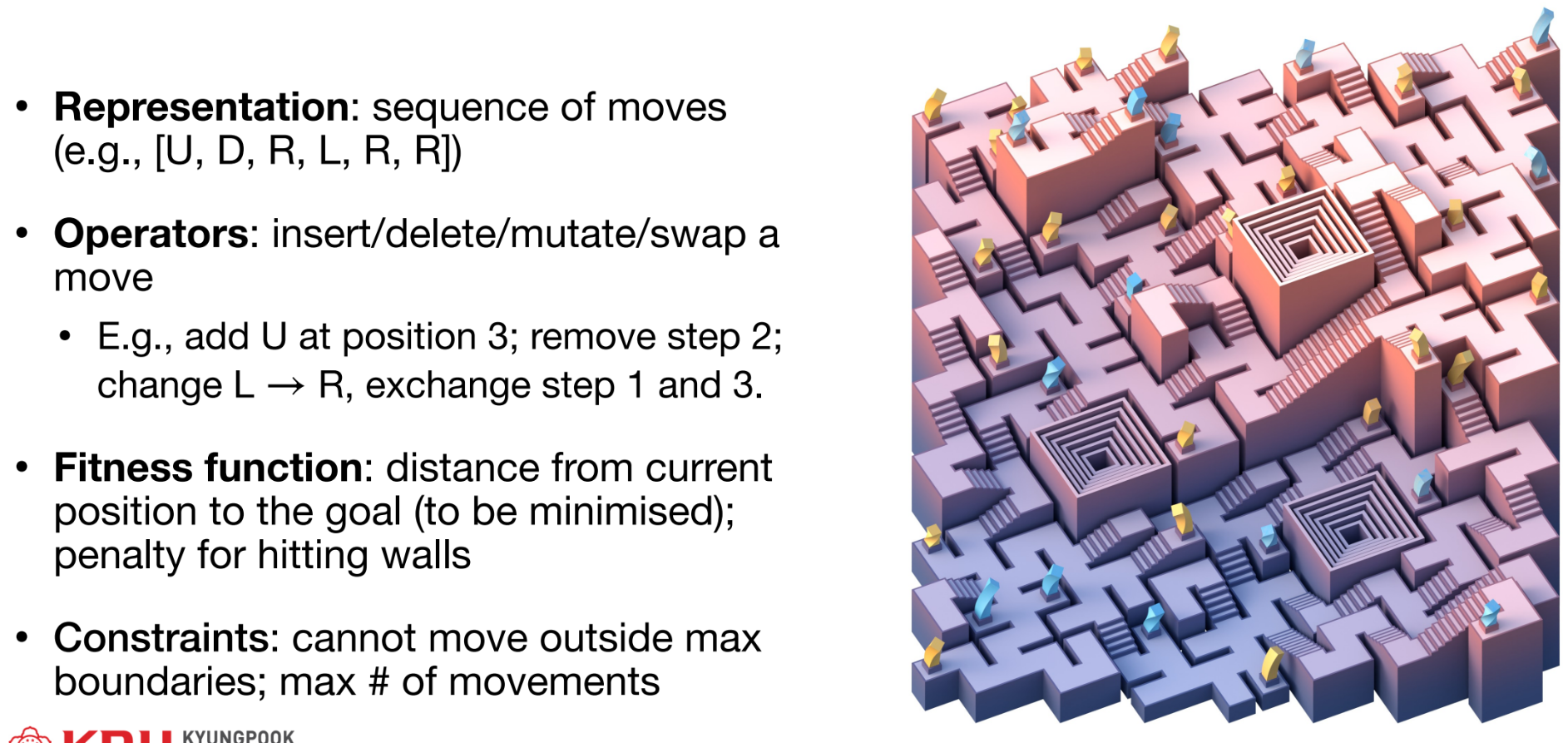

- 연산자 (Operators):
- "이전 시도와 어떻게 다르게 할 것인가?" 즉, 현재 해(solution)에서 새로운 이웃 해(neighboring solution)를 생성하는 방법이다.
- 이 Operators는 검색 공간을 탐색하는 방식을 정의한다.
- 예: 8-Queens 문제에서 퀸 하나의 위치를 다른 칸으로 옮기는(move) 연산자. 자동 패치 생성에서 코드 라인을 삭제(delete)하거나, 다른 라인과 교체(swap)하는 연산자.
- 적합도 함수 (Fitness Function / Objective Function):
- "이번 시도는 얼마나 잘했는가?" 즉, 생성된 해가 얼마나 좋은지를 정량적으로 평가하는 척도이다.
- 이 Fitness Function은 검색 과정을 "안내하는" 유일한 지표가 된다. Metaheuristics는 이 함수의 값을 최대화하거나 최소화하는 방향으로 작동한다.
- 예: 8-Queens 문제에서 서로 공격하는 퀸의 쌍(pair)의 수(최소화 목표). 자동 패치 생성에서 통과하는 테스트 케이스의 수(최대화 목표).
- 제약 조건 (Constraints):
- "반드시 지켜야 할 규칙"으로, 해가 유효(valid)하기 위해 충족해야 하는 조건들이다.
- 제약 조건을 위반한 해는 Fitness Function에서 페널티를 받거나, 생성 과정에서부터 배제될 수 있다.
- 예: 자동 패치 생성 시, 수정된 코드는 반드시 컴파일에 성공해야 한다. 8-Queens 문제에서 퀸은 8개여야 한다.
3. 주요 개념: 탐험 (Exploration) vs. 활용 (Exploitation)
Metaheuristics 검색의 성공은 Exploration과 Exploitation이라는 두 가지 상반된 힘 사이의 균형에 달려있다.

- 탐험 (Exploration):
- "더 넓게 찾기" 전략
- 현재 해와 거리가 먼, 검색 공간(search space)의 새로운 영역을 적극적으로 탐색하여 다양성(diversity)을 확보하는 것을 목표로 한다.
- 이는 지역 최적해(local optimal)에 빠지는 것을 방지하는 데 도움을 준다.
- 지나칠 경우: 좋은 해를 찾았음에도 불구하고 계속 다른 곳만 탐색하므로, 수렴 속도가 매우 느려지거나 무작위 검색(random search)과 다를 바 없게 된다.
- 활용 (Exploitation):
- "더 깊게 파기" 전략
- 현재까지 찾은 해 중에서 가장 유망해 보이는 해(solution)의 주변(neighborhood)을 집중적으로 탐색하여 더 나은 해를 찾으려는 시도이다.
- 이는 검색을 특정 방향으로 수렴(converge)시키는 역할을 한다.
- 지나칠 경우: 처음 발견한 그럴싸한 해(그것이 local optimal일지라도)에 너무 빨리 수렴하여, 검색 공간의 다른 영역에 존재할 수 있는 더 좋은 전역 최적해(global optimal)를 놓치게 된다.
- 핵심 과제: 모든 Metaheuristics 알고리즘의 핵심 설계 과제는, 검색 초기에는 Exploration을 통해 넓게 탐색하고, 후기에는 Exploitation을 통해 좋은 해를 다듬어가는 균형점을 찾는 것


4. 소프트웨어 공학(SE)에서의 적용과 한계
- SE 적용 이유:
- 현대 소프트웨어 시스템은 수백만 라인의 코드로 이루어져(large scale), 매우 복잡하며(complex) 수동으로 모든 것을 처리하는 것이 불가능하다.
- Metaheuristics는 이러한 대규모 SE 문제를 검색 문제(search problem)로 재정의하여 실용적인 해결책을 찾는 데 사용된다.
- 적용 분야: 자동화된 테스트 케이스 생성(automated test generation), 자동 프로그램 복구(Automated Program Repair, APR), 테스트 스케줄링 최적화, 리팩토링(refactoring) 추천 등.
- 함정과 도전 과제:
- 기계의 "게으른" 특성: 기계(알고리즘)는 우리가 정의한 Fitness Function을 만족시키는 가장 쉬운 해를 찾으려는 경향이 있다. 이는 인간 개발자가 의도한 "올바른" 해와 다를 수 있다.
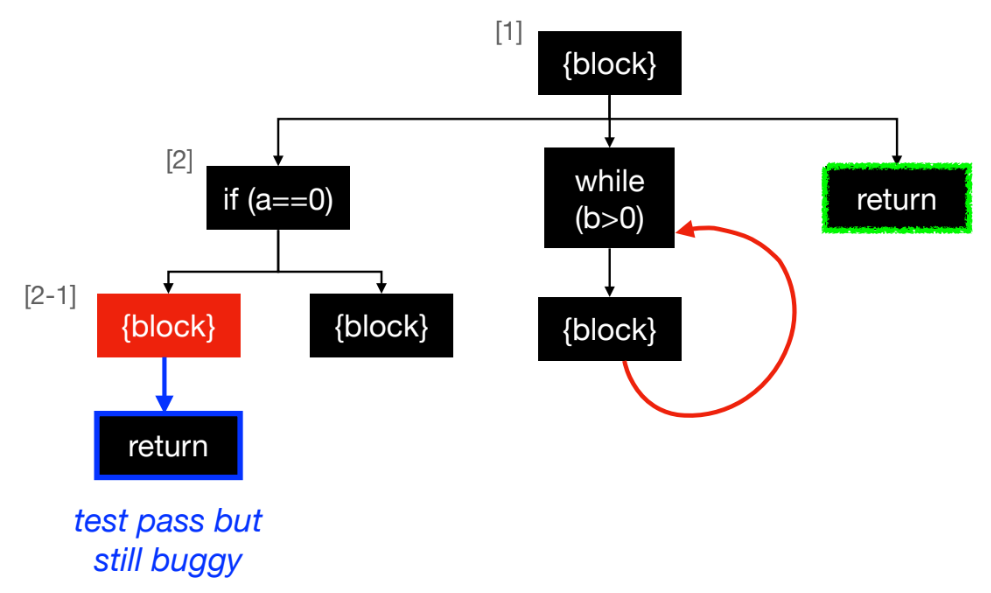
- 잘못된 긍정 (False-Positives): Fitness Function이 불완전할 때 발생한다. 예를 들어, 자동 프로그램 복구(APR) 분야의 GenProg 사례가 대표적이다.
- 사례: Fitness를 "모든 테스트 케이스 통과"로 설정했더니, 알고리즘이 버그를 고치는 대신 버그를 유발하는 코드 라인 자체를 삭제하거나, 아예 빈 값을 반환하도록 수정하여 테스트를 통과시켰다.
- 결과: 테스트는 통과하지만(Fitness ↑), 실제로는 기능이 삭제되거나 의미론적으로 완전히 틀린(semantically wrong) 패치가 생성된다.
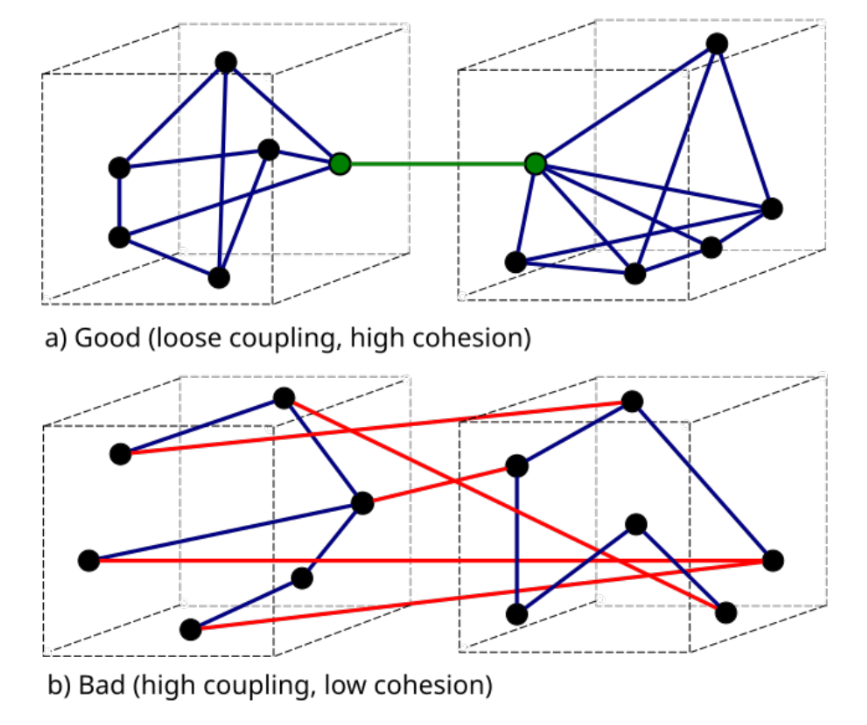
- 구문 (Syntax) vs. 의미 (Semantic)의 괴리:
- Metaheuristics는 대부분 코드의 구조(AST), 라인 수, 커플링(coupling) 같은 구문적(syntactic) 정보를 바탕으로 Representation과 Operators를 설계하고 최적화를 수행한다.
- 하지만 소프트웨어의 진짜 '품질(quality)', '정확성(correctness)', '유지보수성(maintainability)'은 코드의 의미(semantic), 즉 "어떻게 동작하는가"에 달려있다.
- Syntactic인 지표를 최적화하는 것이 항상 Semantic인 품질 향상을 보장하지는 않는다는 것이 SE 분야의 핵심적인 도전 과제이다.
Ecolutinary Comptation
1. Metaheuristics 및 SBSE 복습
Metaheuristics는heuristics를 더 나은 솔루션으로 안내하는 일반적인 프레임워크이다.Metaheuristics의 3가지 핵심 요소는 다음과 같다.Representation: 이번에 무엇을 시도할 것인가.Operators: 이전과 어떻게 다른가.Fitness/objective function: 이번에 얼마나 잘했는가.- (선택적 요소:
constraints- 절대 깨뜨릴 수 없는 규칙).
Search Based Software Engineering (SBSE)는 가이던스가 있는 또 다른 탐색 알고리즘으로 구성될 수 있다.SBSE의 3가지 핵심 요소는 다음과 같다.Representation: 후보 솔루션을 어떻게 표현하고 저장할 것인가.Operators: 후보 솔루션을 어떻게 수정하여 탐색할 것인가.Fitness/objective function: 후보 솔루션을 어떻게 비교하여 선택할 것인가.
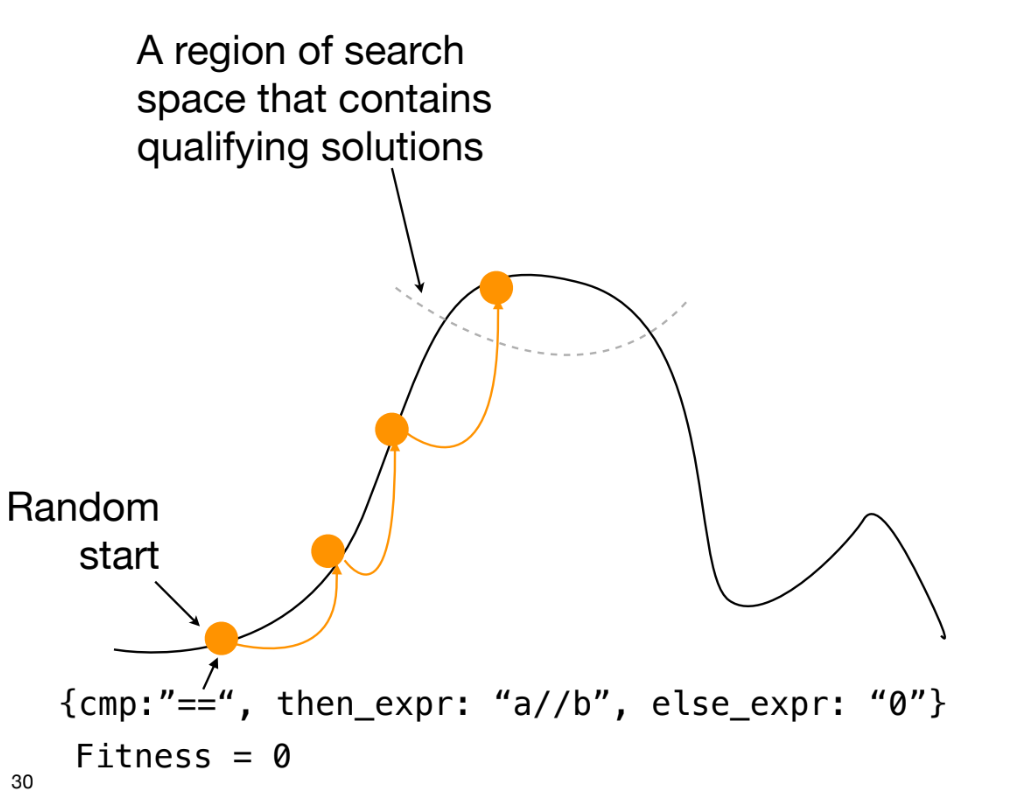
2. Fitness Landscape
Fitness Landscape는 탐색에 대한 공간적 관점을 제공하며, 가능한 솔루션들에 대한fitness분포를 시각화하는 유용한 도구이다.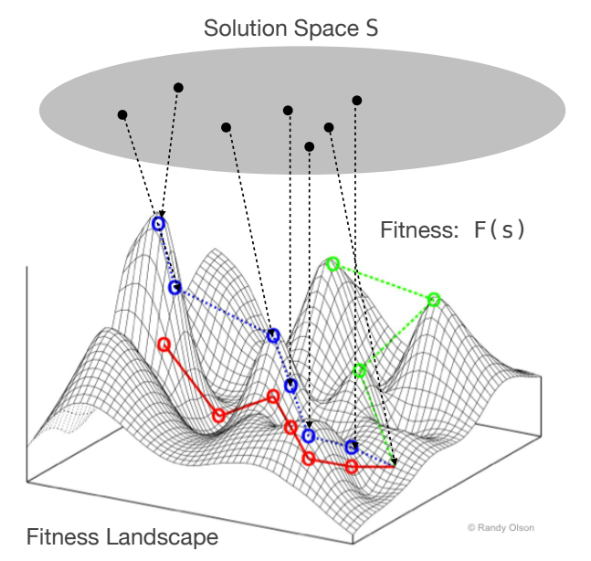
Solution Space S와fitness function F가 주어졌을 때,Fitness Landscape는 을 나타내는 초차원 표면이다.- 예시 문제: 범위에서 을 만족하는 를 찾는 경우.
- 현재 합계 일 때, 해로부터의 거리는 이다.
- 따라서
fitness function은 로 정의할 수 있으며, 이 함수 값을 0으로 최소화하는 것이 목표이다.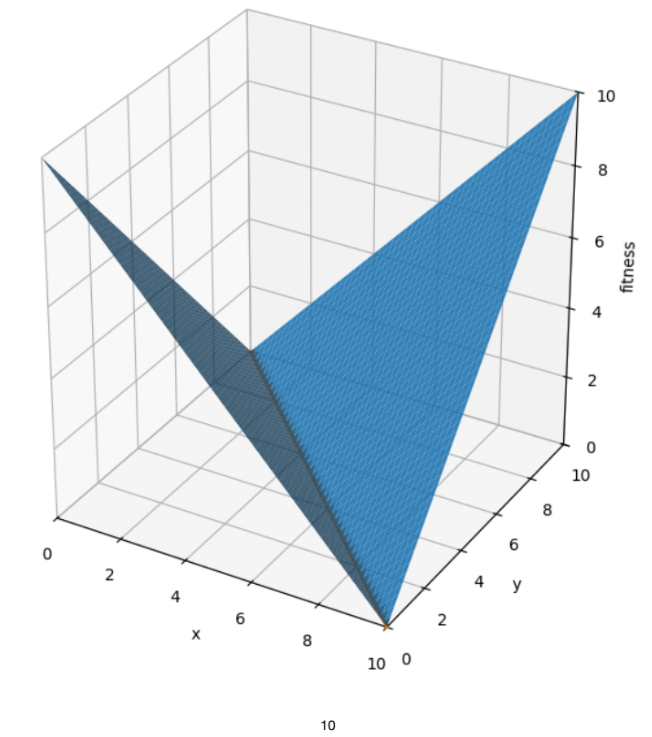
3. Fitness Landscape의 속성
Fitness Landscape는 탐색 난이도에 영향을 미치는 여러 속성을 가진다.- 고유 속성:
Size: 탐색 공간의 크기 (유한/무한).Discreteness: 연속적, 이산적, 또는 조합적(예: 순열, 그래프) 특성.
- 탐색 난이도 관련 속성:
Flatness(Plateau): 기울기(gradient)가 없는 넓고 평평한 지역이다.Plateau에 빠지면 탐색을 위한 가이드가 없어 탈출하기 어렵다.Ruggedness / Smootheness:local optima(지역 최적해)의 수.Smooth Landscape는 최적해로의 하강(descent)이 용이하다.Rugged Landscape는 많은local optima를 가져 탐색이 쉽게 갇힐 수 있다.
Local optima는 주변 영역보다fitness가 좋지만 전체에서 최고는 아닌 해를 의미한다.Global optima는landscape전체에서 가장fitness가 좋은 해를 의미한다.
Needle in the Haystack:- 탐색하기 가장 나쁜 형태의
landscape이다. - 이는
fitness function을 더 잘 설계하여 피할 수 있다. - 예: 을 찾을 때, 는 가이드가 전혀 없지만, 는 최적해 방향으로 명확한 가이드를 제공한다.
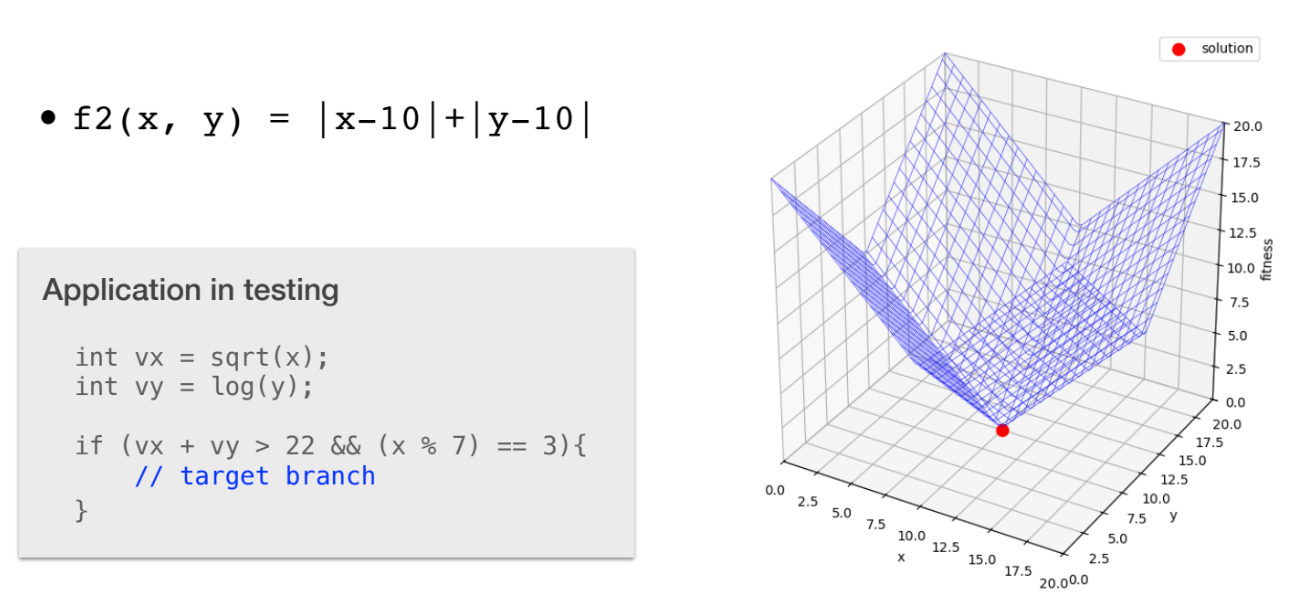
- 탐색하기 가장 나쁜 형태의
4. Discrete Fitness Landscape
- 숫자(numeric)가 아닌 솔루션의 경우 이웃(neighbors)의 정의가 달라진다.
- Set membership (예: 테스트 케이스 포함 여부): 이웃은 하나의 포함 비트(bit)를 뒤집어(flipping) 정의된다.
- Permutations (예: 테스트 스위트 실행 순서): 이웃은 인접 항목을 교환(swapping)하거나 위치를 바꾸어 정의된다.
- Highly structured data (예: 컴파일러 입력 프로그램): 이웃은
synatic(구문적) 또는semantic(의미적) 변경(예:mutation)을 적용하여 정의된다.
5. Random Search와 Local Search
Random Search:- 결정론적 탐색의 정반대이다. 주어진 예산 내에서 무작위 솔루션을 반복 생성하고 가장 좋은 것을 기록한다.
- 장점: 구현이 쉽고, 자동화 가능하며, 편향(bias)이 없다.
- 단점: 가이드가 전혀 없다.
- 새로운 탐색 방법론의 성능 비교를 위한
baseline(sanity check)으로 사용된다. Fuzzing은Random Search의 한 예시로,Infinite Monkey Theorem에 기반하여 프로그램 충돌을 유발하는 무작위 입력을 찾는다.
Local Search:- 무작위 솔루션(들)에서 시작한다.
- 현재 솔루션의 이웃 솔루션(neighouring solutions)들을 고려한다.

- 더 나은 솔루션이 존재하면 이동하고, 그렇지 않으면 멈춘다.
Hill Climbing은Local Search의 대표적인 예시이다.Steepest ascent: 모든 이웃을 평가하여 가장fitness가 좋은 이웃으로 이동한다.First ascent: 이웃 중 현재보다 더 나은 첫 번째 이웃으로 즉시 이동한다.Random ascent: 더 나은 이웃들의 집합(N')에서 무작위로 하나를 선택하여 이동한다.
Local Search가local optimum에 갇혔을 때의 전략:Random restart: 예산(시간 또는fitness평가 횟수)이 남았다면, 다른 무작위 지점에서 탐색을 다시 시작한다.Tabu Search:local optima를 탈출하고 순환(cycling)을 피하기 위해memory structure(Tabu list)를 도입한다. 최근 방문했던 솔루션으로는 (설령 더 나쁜 옵션이더라도) 돌아가지 않도록 금지(tabu)한다.
6. Evolutionary Computation (EC) 소개
Local Search가 단일 무작위 솔루션에서 시작하는 반면,Evolutionary Computation (EC)는 여러 솔루션으로 구성된Initial Population에서 시작한다.
EC는 자연 진화(natural evolution)에서 영감을 받은metaheuristic알고리즘 계열이다.- 후보 솔루션이 세대(generations)에 걸쳐
selection,variation,survival을 통해 진화한다. EC는Mendelism(형질의 상속 및 인코딩)과Darwinism(변이 및 적자생존)의 원리를 결합한다.
7. EC의 이론적 기반: Mendelism과 Darwinism
Mendelism(How: 상속 메커니즘):- 형질이 "genes"(Mendel은 "factors"라 칭함)라는 이산적 유전 단위를 통해 상속되는 방식을 설명한다.
Law of Segregation(분리의 법칙): 생식 중 대립 유전자(alleles) 쌍이 분리되어 자식에게 무작위로 하나가 전달된다.Law of Independent Assortment(독립 배분의 법칙): 서로 다른 형질(예: 색상, 꼬리 길이)의 유전자들은 독립적으로 전달된다.Law of Dominance(우열의 법칙): 우성 대립 유전자가 열성 대립 유전자의 발현을 가린다.
Darwinism(Why: 변화 원리):Variation(변이)과Natural Selection(자연 선택, 즉 적자생존)에 기반하여 종의 진화를 설명한다.- 자연 진화는 목표가 없지만,
EC는optimisation이라는 명확한 목표를 가진다.
EC는Mendelism의 원리(variation operators)를 사용하고,Darwinism의 원리(Variation+Selection)를 통해optimisation을 수행한다.
8. Genotype vs. Phenotype
Genotype: 솔루션의 인코딩된 표현이다. (예: bit string, vector, tree structure)Phenotype:Genotype이 디코딩되어 실제 문제 도메인에서 발현된 솔루션 인스턴스이다. (예: 실제 선택된 테스트 케이스, 프로그램 패치)- 0-1 Knapsack Problem 예시:
Genotype: N개의 아이템 각각을 선택했는지(1) 아닌지(0)를 나타내는 bit string.Phenotype: 배낭에 담긴 아이템들의 총 무게와 총 가치.
- Automated Program Repair 예시:
Genotype: AST tree edits의 시퀀스.Phenotype: 컴파일되고 실행되는, 버그가 수정된 프로그램.
9. EC의 핵심 개념 및 절차
Evolutionary Pressure(진화 압력):- 번식 성공률(reproductive success rate)에 영향을 미치는 모든 요소를 의미한다.
EC에서는fitness가 높은 개체가 더 나은 번식 성공률을 갖는다고 가정하여optimisation을 유도한다.- 이는
exploitation(활용)과exploration(탐험) 사이의 균형과 밀접하게 연관된다. - 압력이 너무 높으면:
premature convergence(조기 수렴)가 발생하여local optimum에 갇힌다. - 압력이 너무 낮으면: 탐색이 방향성을 잃고 무작위 탐색처럼 된다.
EC개요 순서도: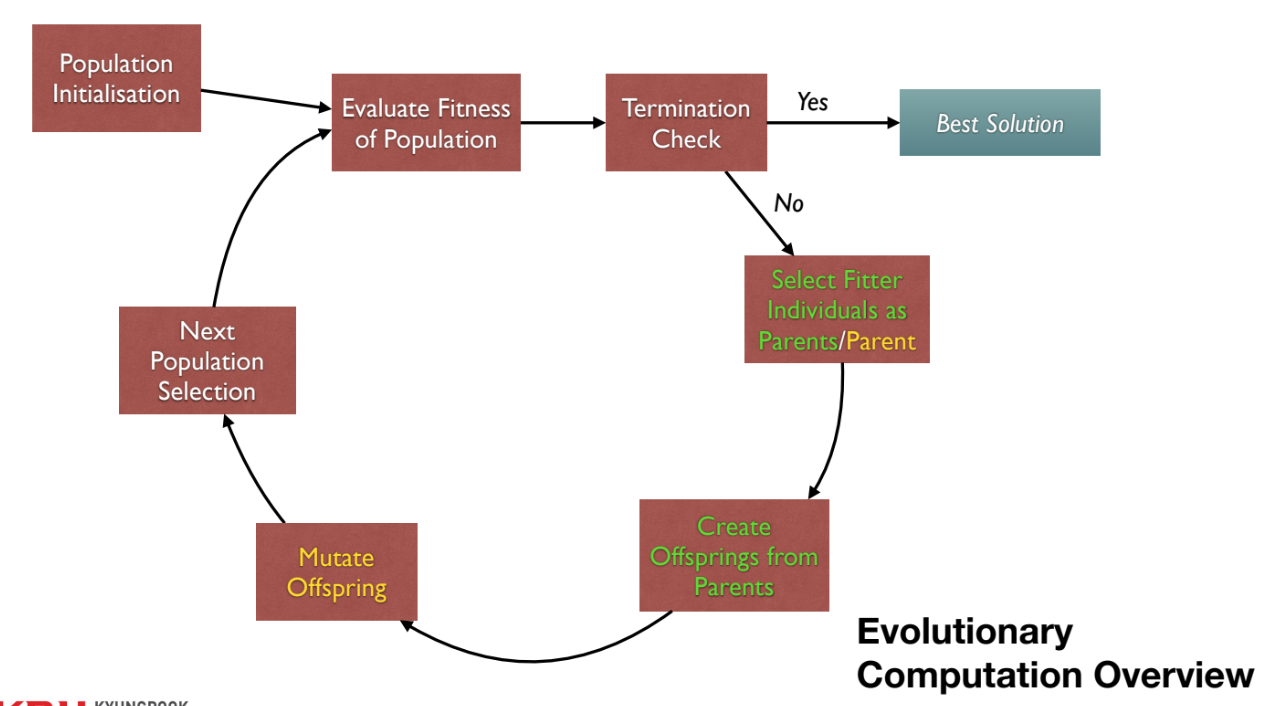 1.
1. Population Initialisation: 초기 집단을 생성한다. 2.Evaluate Fitness of Population: 집단 내 모든 개체의fitness를 평가한다. 3.Termination Check: 종료 조건(예: 시간, 세대 수)을 확인한다. (Yes)Best Solution을 반환한다. 4. (No)Select Fitter Individuals as Parents:fitness가 높은 개체들을 부모로 선택한다. 5.Create Offsprings from Parents: 부모로부터 자손(offsprings)을 생성한다 (예:crossover). 6.Mutate Offspring: 자손을 변이시킨다 (예:mutation). 7.Next Population Selection: 다음 세대를 구성할 집단을 선택한다. 8. 2번 단계로 돌아가 반복한다.EC구성 요소:Gene(유전자)와Allele(대립 유전자)가 모여Chromosome(염색체), 즉Genotype을 이룬다. 이는Phenotype(솔루션)으로 디코딩되며,fitness값을 갖는다. 이 개체(Individual)들이 모여Population을 구성한다.
10. Genetic Algorithm (GA)
GA는EC의 대표적인 기본 알고리즘이다.- 개별 솔루션(individual)은
chromosomes(염색체)로 인코딩되며, 주로 고정 길이의 bit-strings나 array를 사용한다. crossover(교차)를 주된 탐색 연산자로 강조하며mutation(돌연변이)이 보조 역할을 한다.- 6자리 비밀번호(예: 893714) 찾기 예시:
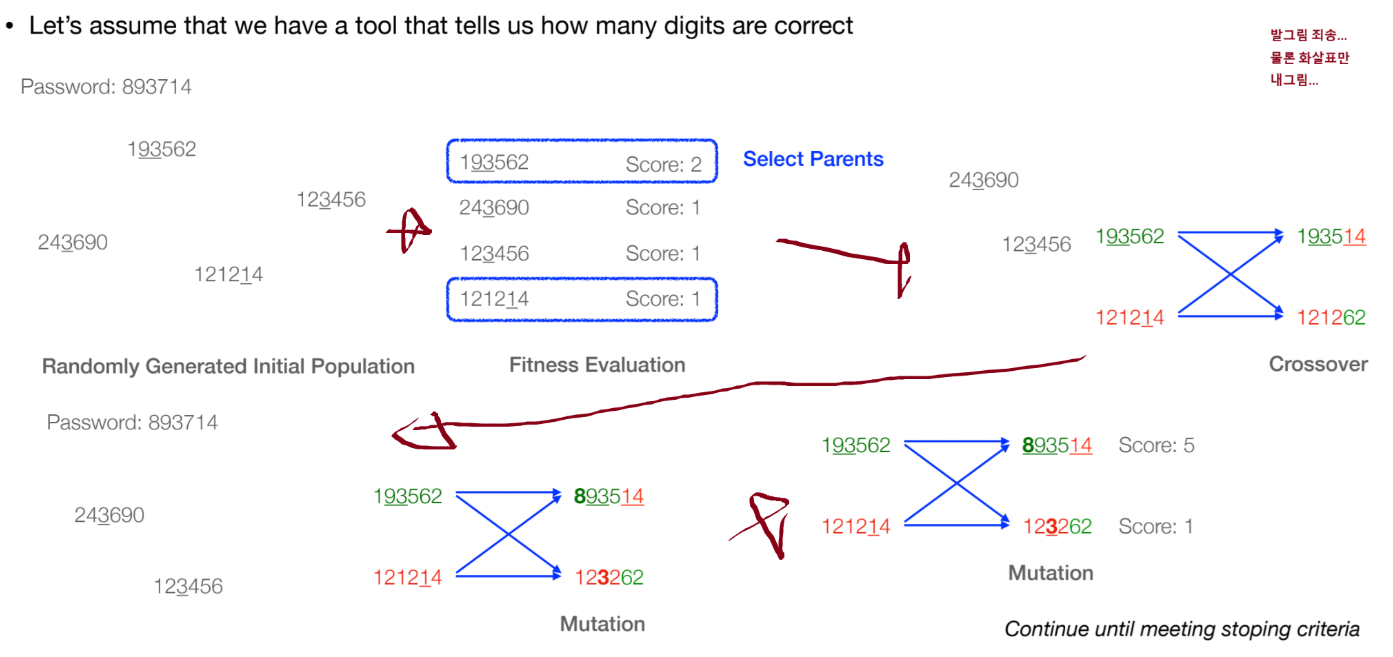 1. 초기 집단 무작위 생성 (예: 193562, 123456) 2.
1. 초기 집단 무작위 생성 (예: 193562, 123456) 2. Fitness평가 (맞는 자리 수, 예: 193562 -> Score 2) 3. 부모 선택 (예: 193562, 121214) 4.Crossover: 부모chromosome의 일부를 교환하여 자손 생성 (예: 1935|62 + 1212|14 -> 193514, 121262) 5.Mutation: 자손chromosome의 일부를 무작위로 변경 (예: 193514 -> 893514) 6. 새로운 자손 평가 (예: 893514 -> Score 5) 7. 종료 조건(예: Score 6 또는 최대 세대)까지 반복. Initial Population은phenotype variance(표현형 다양성)를 도입하기 위해 무작위로 생성한다.
11. Selection Operators
Selection operators는evolutionary pressure를 적용하여 부모 개체를 선택하는 방법이다.Fitness Proportional Selection (FPS):- 선택 확률이 절대적인
fitness값에 정비례한다. Roulette Wheel Selection (RWS)은FPS의 일반적인 구현 방식이다.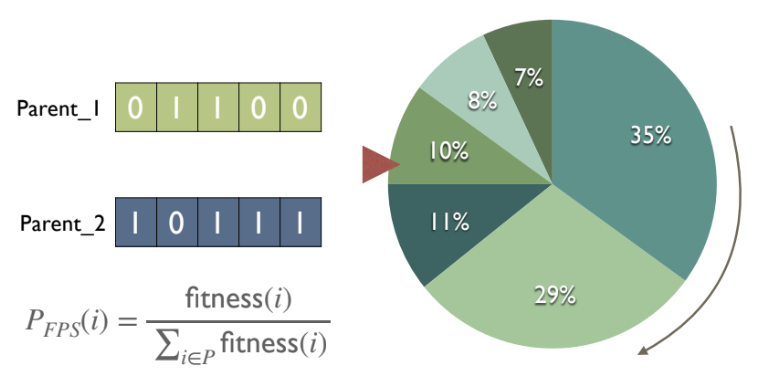
FPS의 문제점:fitness가 월등히 높은 개체가 집단을 빠르게 장악하여premature convergence를 유발할 수 있다.fitness값의 범위가 좁으면(예: 모든 개체의fitness가 100~110 사이) 선택 압력이 거의 사라진다.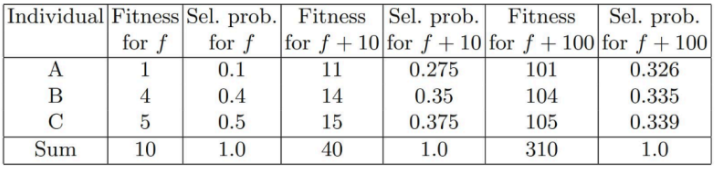
- 선택 확률이 절대적인
Stochastic Universal Sampling (SUS):RWS를 여러 번 독립적으로 수행할 때 발생할 수 있는 편향(우연히fitness가 높은 개체가 몰아서 선택됨)을 줄이기 위한 방식이다.- 룰렛 휠에 여러 개의 동일한 간격의 포인터를 사용하여 한 번의 '스핀'으로 여러 개체를 공평하게 샘플링한다.
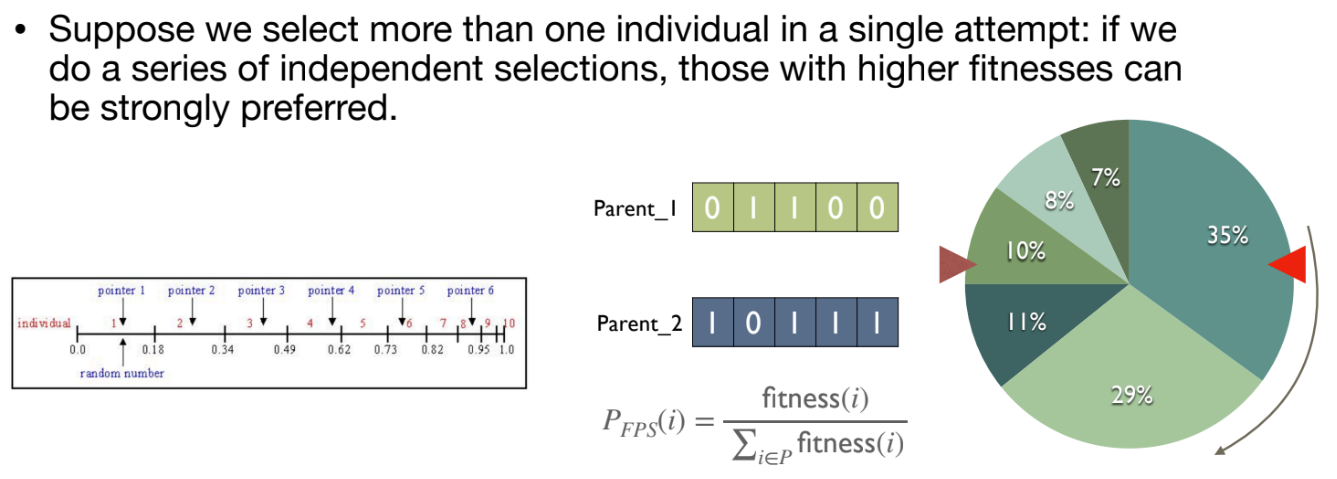
Ranking Based Selection:FPS의 문제를 해결하기 위해, 절대fitness값이 아닌rank(순위)를 기준으로 선택 확률을 할당한다.fitness값의 실제 분포와 관계없이 일정한 선택 압력을 유지할 수 있다.Linear Ranking과Exponential Ranking방식이 있다.
Tournament Selection:k개의 개체를 집단에서 무작위로 선택하고, 그중 가장fitness가 좋은 개체를 선택(승자)한다.k(토너먼트 크기)가 커질수록 선택 압력이 증가한다.- 절대적인
fitness값을 계산하기 어렵거나(예: 전략 게임), 분산 환경에서 전역fitness정보를 알기 어려울 때 유용하다. - 가장 간단하고 널리 사용되는 방식이다.
Overselection:- 의도적으로
fitness가 좋은 개체들(예: 상위 20%)에서 더 많은 비율(예: 80%)의 선택을 수행하여, 선택 압력을 직접적으로 증폭시키는 방식이다.
- 의도적으로
Evolutionary Computation-SBSE
1. Evolutionary Computation (EC) 개요
Evolutionary Computation (EC)는 자연적인 진화 과정을 모방한 최적화 기법이다. 전체적인 프로세스는 다음과 같은 순환 구조를 가진다.
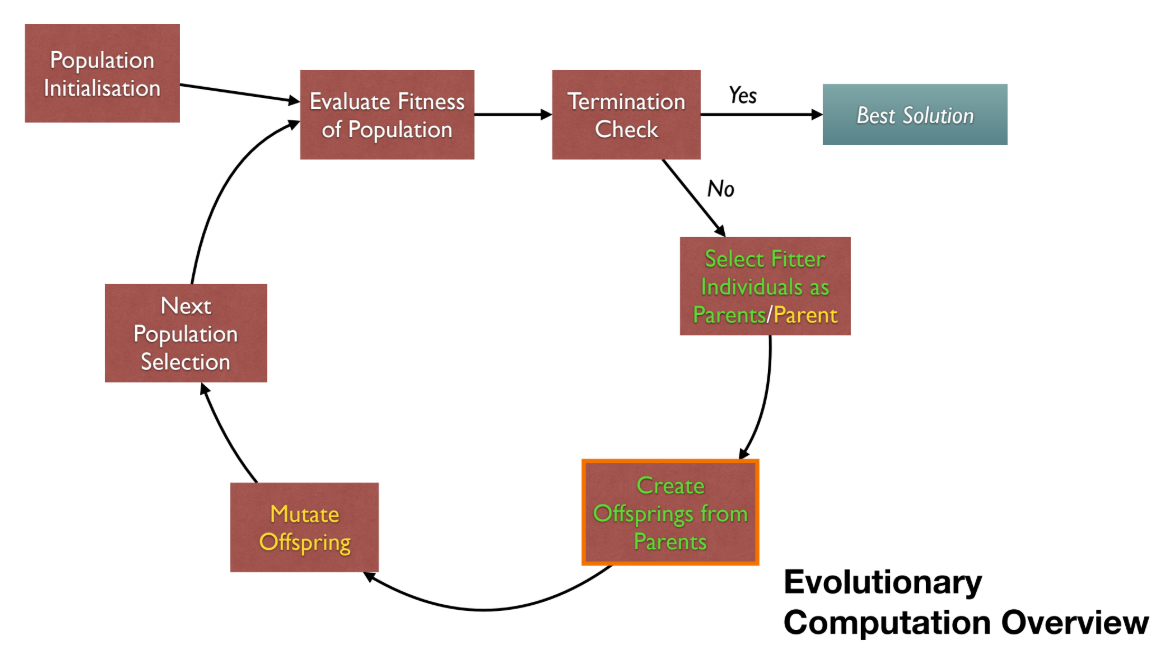
- Population Initialisation: 해(solution)가 될 수 있는 개체(individual)들의 초기 집단(population)을 생성한다.
- Evaluate Fitness of Population: 각 개체가 얼마나 좋은 해인지를 평가하는 Fitness 함수를 통해 집단을 평가한다.
- Termination Check: 종료 조건을 확인한다 (예: 특정 세대 수 도달, 만족스러운 해 발견).
- Yes: 가장 좋은 해(Best Solution)를 반환하고 종료한다.
- No: 다음 단계로 진행한다.
- Select Fitter Individuals as Parents: Fitness가 높은 개체들을 부모(Parents)로 선택한다.
- Create Offsprings from Parents: Crossover 연산자를 사용해 부모로부터 자손(Offsprings)을 생성한다.
- Mutate Offspring: Mutation 연산자를 사용해 자손을 일부 변형한다.
- Next Population Selection: 생성된 자손과 기존 개체들을 조합하여 다음 세대의 집단을 선택한다.
- 다시 'Evaluate Fitness of Population' 단계로 돌아가 반복한다.
2. 핵심 연산자: Crossover
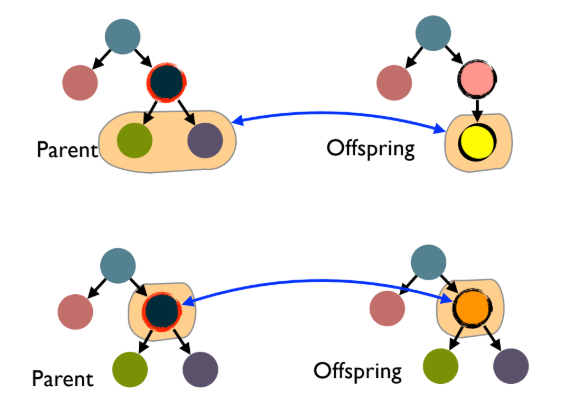
Crossover (교배) 연산자는 부모 개체들의 유전 정보(genotype)를 재조합하여 자손을 생성하는 과정이다.
- 자손은 부모의 유전자를 물려받지만, 동일한 형태는 아니다.
- 이는 멘델의 유전 법칙과 유사하게 유전자형(genotype) 전체를 재조합하는 방식이다.
- 표현 방식에 따라 다양한 Crossover 방식이 존재한다.
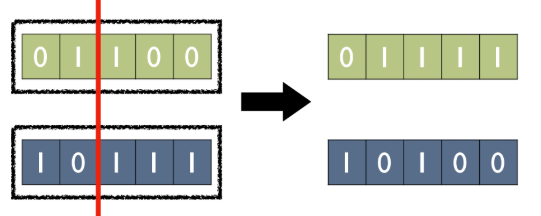
- Bit-strings: 1-point Crossover는 부모의 비트 문자열에서 임의의 지점을 선택하여 해당 지점 이후의 비트들을 교환한다.
- Real-valued vectors: 두 부모 벡터의 값들을 조합 (예: 평균)하여 새로운 자손 벡터를 생성한다.
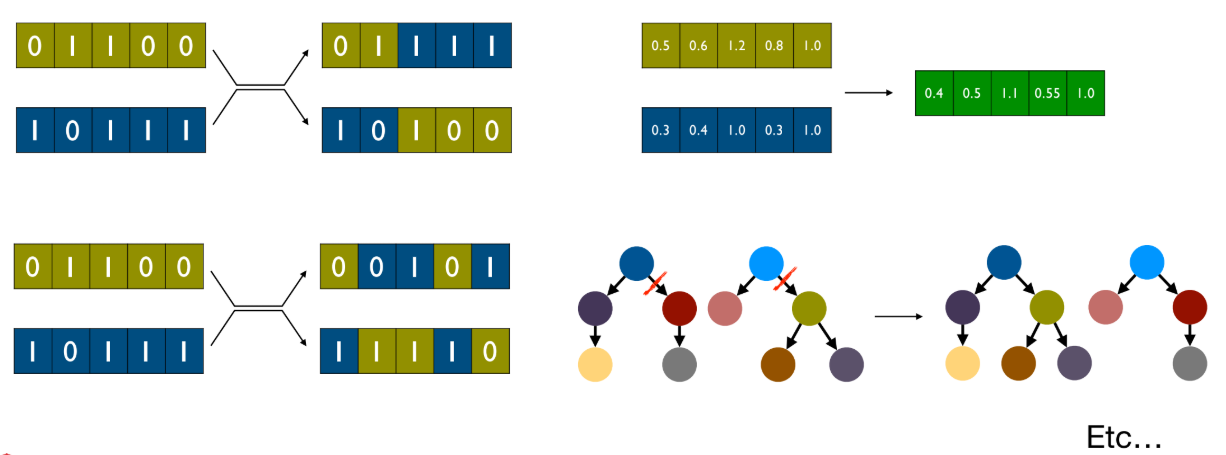
3. Genetic Programming (GP)
Genetic Programming (GP)은 EC의 한 분야로, 자연 진화를 모방하여 프로그램을 자동으로 생성하고 문제를 해결하는 기법이다.
- GP는 프로그램의 집단(population of programs)에 대해 연산을 수행한다.
- 개별 개체(Individual)가 곧 프로그램(program)이며, 이는 비선형적인 트리(tree) 구조로 표현된다 (예: Abstract Syntax Tree, AST).
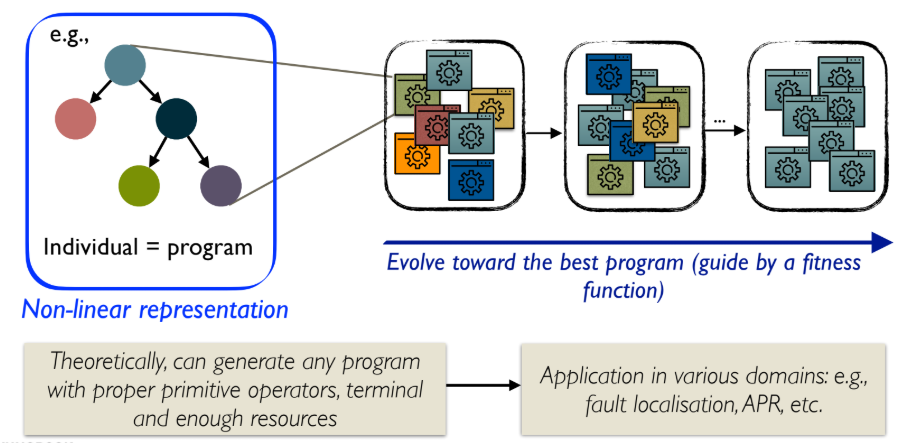
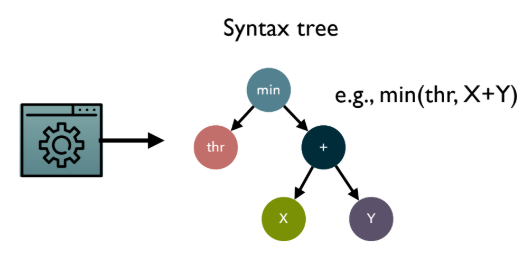
- GP 흐름:
- 무작위 프로그램 집단을 생성한다.
- 프로그램을 실행하고 품질(Fitness)을 평가한다.
- Fitness가 더 좋은 프로그램들을 선택하여 'Breed' (Crossover 및 Mutation)한다.
- 2단계로 돌아가 반복한다.
- GP Crossover:
- GP의 Crossover는 두 부모 트리(program) 간에 서브트리(subtree)를 교환하는 방식으로 작동한다.
- One-point crossover: 두 부모 트리에서 공통 영역(common region)을 찾아 임의의 노드를 선택한 뒤, 해당 노드를 루트로 하는 서브트리 전체를 교환한다.
- Uniform crossover: 공통 영역의 모든 노드를 검사하며 교환 여부를 결정하여 다양성을 높인다.
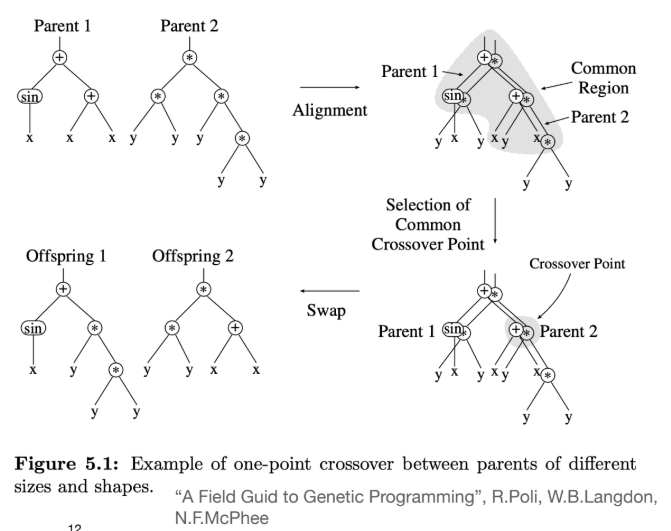
4. 핵심 연산자: Mutation
Mutation (돌연변이) 연산자는 개체의 유전자형에 작은, 국소적인 변형을 가한다.
- Mutation은 집단에 새로운 유전적 물질(genetic material)을 도입하는 유일한 방법일 수 있다.
- Mutation이 없다면, EC는 단지 초기의 무작위 집단에 있던 유전자들을 재조합하는 것에 그친다.
- Crossover만 사용할 경우, 탐색이 지역 최적점(local optimum)에 수렴하여 더 좋은 해를 찾지 못하는 Early convergence 문제가 발생할 수 있다.
- Mutation은 이러한 지역 최적점에서 '탈출(Escape)'하여 탐색 공간의 다른 영역을 탐색할 수 있게 돕는다.

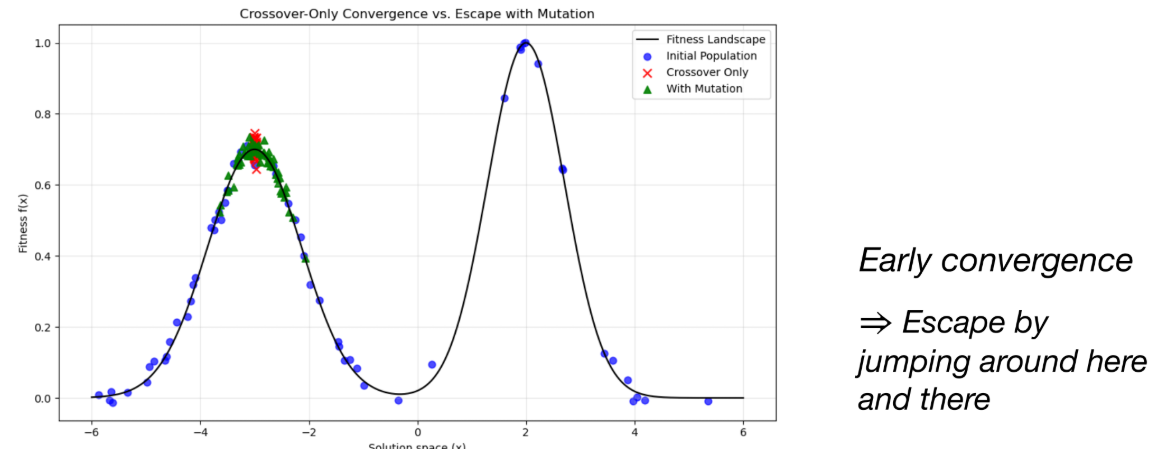
- Mutation 예시:
- Single bit-flip (0을 1로, 1을 0으로 변경)
- 정수 값에 작은 값 더하기/빼기
- 순열(permutation)에서 두 요소의 위치 교환(swap)
- GP Mutation:
- Subtree mutation: 임의로 선택한 서브트리를 무작위로 생성된 다른 서브트리로 교체한다.
- Node replacement mutation: 트리의 노드 하나를 임의로 선택하여, 인자(argument) 수가 동일한 다른 호환되는 노드로 교체한다.
5. EC 프로세스 구성 요소
5.1. Generational Selection
다음 세대의 집단을 선택하는 과정이며, 또 다른 진화적 압력(Evolutionary pressure)으로 작용한다.
- Generational Replacement: 부모 세대는 모두 버리고, 생성된 자손들로만 다음 세대를 구성한다.
- Elitism: 부모 세대에서 가장 우수했던 M개의 개체를 다음 세대에 그대로 유지한다. (이유: Fitness 평가의 노이즈, 강한 Mutation으로 인한 우수해 손실 방지)
- Gradual Replacement: 부모 세대에서 가장 열등한 M개의 개체를 자손 세대에서 가장 우수한 M개의 개체로 교체한다. (이유: 급격한 교체를 피하고 좋은 해를 유지)
5.2. Termination: Stopping Criterion
종료 조건을 결정하는 것은 어려울 수 있다. EC는 확률적(stochastic) 알고리즘이며, 전역 최적점(global optimum)이 무엇인지 알 수 없기 때문이다.
- 현실적인 종료 조건:
- Fixed number of fitness evaluations: 미리 정해둔 Fitness 평가 횟수(또는 세대 수)에 도달했을 때.
- Good enough solution: 충분히 만족스러운 품질의 해를 찾았을 때.
5.3. Parameters
EC는 고정된 답이 없는 많은 파라미터(parameter)들을 튜닝해야 한다.
- 예: Population size, Crossover 및 Mutation 적용 빈도(rate), Elitism에서 유지할 개체 수(M), 최대 반복 횟수 등.
- 이 파라미터들은 복잡하고 비선형적인 상호작용을 한다. (예: 높은 Crossover rate + 높은 Selection pressure = Early convergence)
- 이는 마치 사운드 믹서의 수많은 노브(knob)를 조절하는 것과 유사하다.

6. EC의 유용성 및 이론적 배경
6.1. EC의 유용성
- Black-box optimisation: 최적화하려는 문제의 기울기(gradient)나 미분(derivative) 정보, 또는 내부 구조를 알 필요가 없다. (bit-string, real-valued vector, tree 등 다양한 표현에 적용 가능)
- Exploration + Exploitation balance: Mutation (탐색, Exploration)과 Crossover (활용, Exploitation) 간의 균형을 맞춘다.
- Robustness: 단순한 지역 탐색(local search)보다 지역 최적점에 갇힐(stuck) 가능성이 낮다.
- Population-based: 집단 기반 탐색을 통해 탐색 공간의 여러 영역을 동시에 탐색할 수 있다.
6.2. Schema Theory (GA가 동작하는 이유)
- Schema Theory (John Holland, 1975)는 Genetic Algorithm (GA)이 어떻게 동작하는지 설명하는 이론이다.
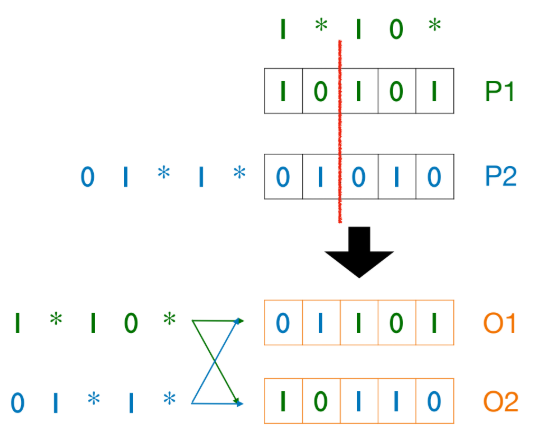
- Schema: 해(solution)의 부분적인 패턴(template)을 나타내며, "don't care" 심볼(*)을 사용한다. (예:
1*10\*) - Schema는 해의 "building blocks" (구성 요소)로 볼 수 있다.
- Selective Reproduction: GA는 (명시적이 아닌) 암묵적으로 유용한 Schema(패턴)를 선택하고 재조합한다.
- 평균 이상의 Fitness를 가진 Schema는 세대가 지남에 따라 집단 내에서 확산되는 경향이 있다.
- Crossover와 Mutation은 이러한 Schema를 파괴(disrupt)할 수 있다.
- "Short, low-order" (길이가 짧고, *가 적은) Schema일수록 Crossover나 Mutation에 의해 파괴되지 않고 생존할 확률이 높다.
7. Search Based Software Engineering (SBSE)와 EC
- Software Engineering (SE): 많은 SE 작업들(예: 어떤 테스트를 먼저 실행할지, 요구사항을 어떻게 배분할지, 코드를 어떻게 리팩토링할지)은 본질적으로 최적화 문제(optimisation problems)이다.
- SBSE: EC와 같은 Metaheuristics 기법을 SE 문제에 적용하는 분야이다.
- SE의 Artefacts (산출물, 예: 테스트 순서, 코드) -> EC의 Candidate solutions (후보 해)
- SE의 Quality metrics (품질 지표, 예: 코드 커버리지, 결함 발견율) -> EC의 Fitness functions (적합도 함수)
8. SBSE 적용 예시: Test Case Prioritisation
8.1. 문제 정의
- Problem: 테스트 스위트(test suite)가 너무 커서 제한된 시간 안에 모든 테스트를 실행할 수 없다.
- Idea: 중요도 순서에 따라 테스트를 실행한다.
- Goal: Maximise early fault detection (결함 조기 발견 최대화). 즉, 테스트가 중간에 중단되더라도 최대한 많은 결함을 빨리 발견하도록 테스트 케이스의 순서를 정한다.
- Simple heuristics: 단순하게 순서를 거꾸로(backwards) 실행하거나 무작위(random)로 실행하는 것만으로도 원래 순서(1~100)보다 나을 수 있다.
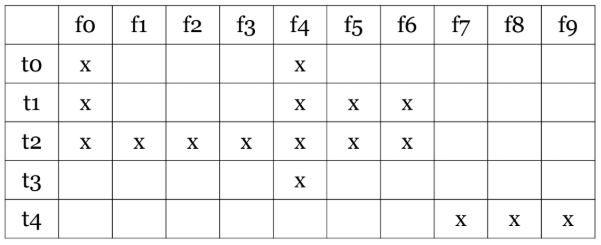
- Ideal (unrealistic) case: 만약 모든 결함(f0
f9)을 어떤 테스트(t0t4)가 잡는지 안다면, 가장 많은 결함을 잡는 t2, 그다음 t4 순서로 실행할 것이다.
8.2. 평가 지표 (Fitness): APFD
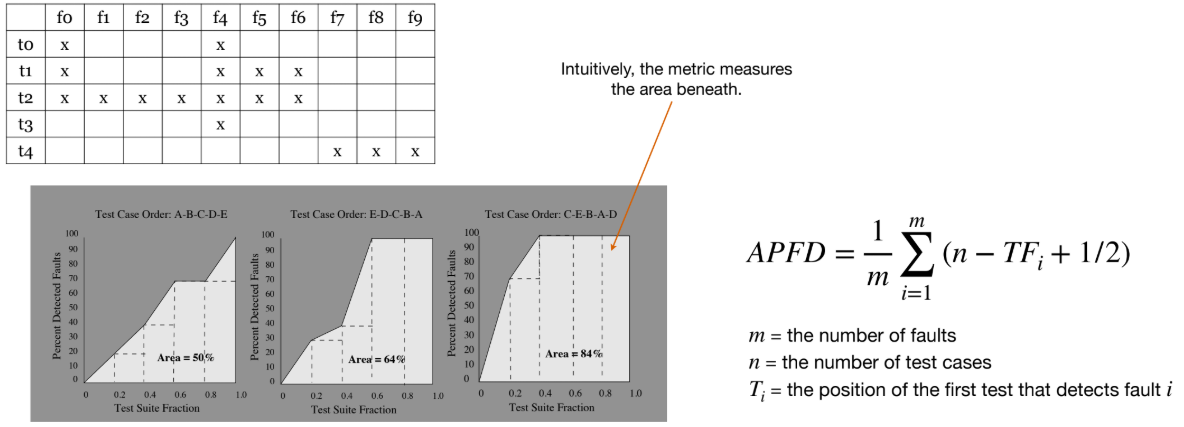
- 테스트 순서가 결함을 얼마나 빨리 감지했는지 측정하는 지표로 Average Percentage of Fault Detection (APFD)를 사용할 수 있다.
- APFD는 '결함 발견율-테스트 스위트 실행 비율' 그래프의 아래 면적을 측정한다. 면적이 넓을수록 (최대 100%) 더 빨리 결함을 발견하는 좋은 순서이다.
8.3. Surrogate: Coverage
- 현실적 한계: 실제로는 어떤 테스트가 어떤 결함을 잡는지 미리 알 수 없다.
- Surrogate (대리 지표): 따라서, 실제 결함 정보 대신 달성하기 쉬운 대리 지표를 사용한다. 가장 흔한 Surrogate는 Coverage이다.
- Structural Code Coverage:
- 결함 감지를 위한 필요조건이지만, 충분조건은 아니다. (실행되지 않은 코드의 결함은 절대 찾을 수 없다)
- 주의: Coverage가 높다고 해서 결함이 없거나 많다는 것을 보장하지는 않는다.
- Coverage는 측정 가능하고(measurable), 수집 비용이 저렴하며(cheap), 일반적인 목적(general-purpose)으로 사용 가능하고, 결함 감지율과 어느 정도 상관관계(correlate somewhat)가 있다.
- Coverage에도 여러 기준이 있으며, 계층 구조를 가진다. (예: Statement < Branch < Condition/Decision < MC/DC < All Paths)


8.4. EC를 이용한 구현
Test Case Prioritisation 문제를 EC로 해결하는 과정은 다음과 같다.
- Task: 테스트 케이스의 순서를 정하여 (Coverage를 사용한) 조기 결함 탐지(대리 지표)를 최대화한다.
- Representation (Genotype/Phenotype):
- 테스트 케이스의 순열(permutation).
- 예: {T0, T1, T2, T3, T4} -> [2, 4, 1, 0, 3] (T2 -> T4 -> T1 -> T0 -> T3 순서)
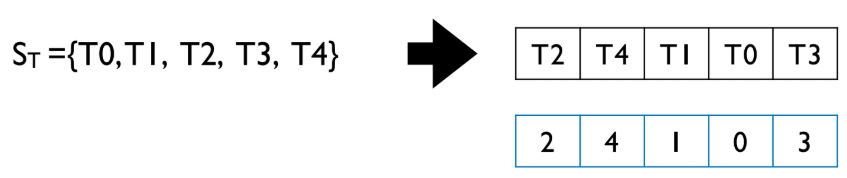
-
Fitness Function:
- Coverage를 Surrogate로 사용한다.
- 예: 각 코드 라인(statement)이 해당 순서(permutation)에서 처음으로 커버되는 테스트의 평균 인덱스(index). (이 경우 값이 낮을수록 좋음 - Minimisation)
-
Operators:
- 순열(permutation)에 적합한 연산자를 사용한다.
- Mutation:
mut_swap- 순서에서 임의의 두 테스트 케이스의 위치를 교환(swap)한다. - Crossover:
cx_ordered- 한 부모(P1)의 일부 순서(T4, T1, T0)를 그대로 가져오고, 나머지 위치는 다른 부모(P2)의 순서를 따르되, 중복되지 않게 채운다.
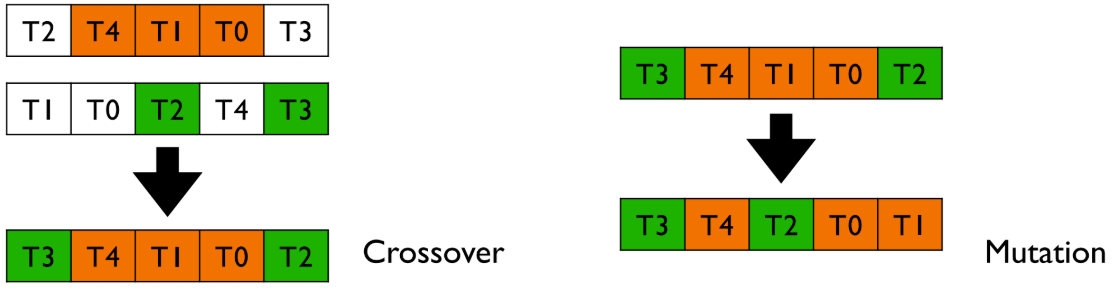
Automated Software Testing
1. 자동화된 소프트웨어 테스팅 소개
1.1. 소프트웨어 테스팅이란?
- 소프트웨어 테스팅(Software testing)은 이해 관계자에게 테스트 대상 제품 또는 서비스의 품질에 대한 정보를 제공하기 위해 수행되는 동적 조사이다.
- 품질이 곧 (기능적) 정확성(Correctness)을 의미하는 것은 아니다.
- 품질에는 신뢰성(Dependability: 정확성, 가용성, 신뢰도 등)과 기타 유형(성능, 사용성, 윤리성)이 포함된다.
1.2. Fairness Testing (공정성 테스팅)
- 테스트 대상 시스템(SUT)이 얼마나 공정한지 체계적으로 평가하는 소프트웨어 테스팅의 하위 분야이며, 주로 AI/ML 기반 시스템에 적용된다.
- 전통적인 테스팅과는 다르며, 입력 그룹의 분포와 대표성, 민감한 기능에 대한 모델 동작, 모델 내부 로직 등을 고려해야 한다.

- 2018년 Joy Buolamwini와 Timnit Gebru의 연구에 따르면, 상용 안면 분석 시스템이 밝은 피부 남성에게는 95% 정확도를 보였으나 어두운 피부 여성에게는 65%의 정확도만 보이는 등 큰 격차를 나타냈다.
1.3. 테스팅 자동화의 차원
- 자동화는 품질이 잘 정의되고, 관찰 가능하며, 점검 가능할 때 가장 잘 작동한다.
- 테스트 오라클(Test oracle, 기대되는 출력)을 정의할 수 있어야 한다.
- 신뢰성(Dependability)은 자동화가 비교적 쉽지만, 비기능적 요소(성능, 사용성, 보안)는 더 어렵고 최신 기술이 요구된다.
2. Fault, Error, Failure
2.1. 테스팅의 목표
- 소프트웨어는 지속적으로 변경되고 진화한다.
- 테스팅은 소프트웨어 시스템의 수명 주기 동안 좋은 품질을 보존하는 것을 목표로 한다.
- 주요 목표 중 하나는 SUT에서 모든 Fault(결함), Error(오류), Failure(실패)를 식별하고 제거하는 것이다.
2.2. 정의
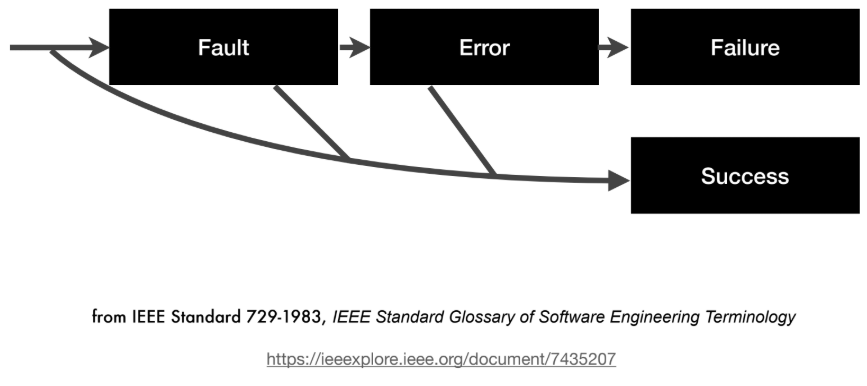
- Fault (결함): 프로그램 소스 코드의 변칙으로, Error를 유발할 수 있다.
- Error (오류): Fault 실행의 런타임 효과로, Failure를 초래할 수 있다.
- Failure (실패): Error가 프로그램 외부에 나타나는 현상이다.
- 인과 관계: Fault → Error → Failure

2.3. 용어의 모호성
- 고전적인 SE(소프트웨어 공학)나 형식적 방법론에서는 (인간의) Error가 (코드 내의) Fault를 유발한다고 보기도 한다.
- 하지만 소프트웨어 테스팅 문맥에서는, (정적인) Fault가 (런타임의) Error(예: 잘못된 변수 값, null 포인터)를 유발한다고 정의한다.
2.4. 예시
- Fault 존재, Error/Failure 없음:
rotateLeft함수 예제에서,size 0으로 테스트하면 결함이 있는 루프가 실행되지 않아 Error나 Failure가 발생하지 않는다. - Error 존재, Failure 없음:
size 2,rgInt [0, 1]로 테스트하면, 루프가 배열 외부 메모리에 접근(Error)하지만, 우연히 출력 배열이 올바르게 나와 Failure는 발생하지 않는다 (Coincidental Correctness). - Failure 발생:
size 2,rgInt [0, 1] 66으로 테스트하면, Error가 발생하고 출력도[1, 66]으로 틀리게 되어 Failure가 발생한다. - Fault의 결정: Fault가 무엇인지는 실제 수정(fix) 내용에 따라 결정된다. 예를 들어
abs(int x)함수가x < 0일 때x를 반환하는 경우,- Fix 1 (
return -x): Fault는 '부정확한 산술 논리'이다. - Fix 2 (
return 0): Fault는 '누락된 입력 유효성 검사'이다.
- Fix 1 (
3. 테스팅의 어려움
3.1. 테스팅 기본 용어
- Test Input: 프로그램을 실행하는 데 사용되는 입력 값 집합.
- Test Oracle: 실제 동작이 예상 동작과 일치하는지 판단하는 메커니즘. 이는 매우 어렵고 노동 집약적인 문제이다.
- Test Case: Test Input + Test Oracle.
- Test Suite: Test Case의 모음.
- Testing vs. Debugging: Testing은 Fault를 드러내고, Debugging은 Fault를 제거한다.
3.2. 난제 1: 결정 불가능성 (Undecidability)
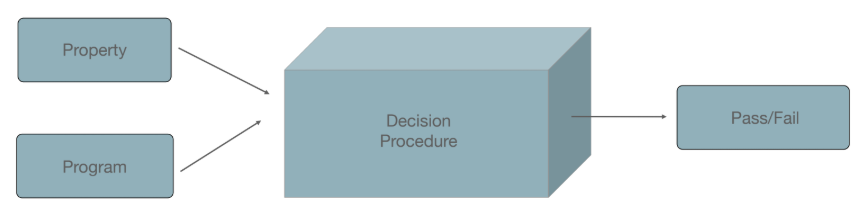
- (정확성 같은) 프로그램의 속성은 결정 불가능하다(Undecidable). 만약 이것이 가능하다면 정지 문제(Halting Problem)를 풀 수 있게 된다.
- 정지 문제는 거의 모든 중요한 비자명적(non-trivial) 속성에 내재될 수 있다.
- Edsger W. Dijkstra: "테스팅은 버그의 존재를 증명할 수 있을 뿐, 부재를 증명할 수는 없다.".
- 이유는 테스팅이 거대한 프로그램 입력 공간의 일부만을 샘플링하기 때문이며, 효과적인 샘플링 방법을 고안하기 어렵기 때문이다.
3.3. 난제 2: 테스트 오라클 문제

- 오라클 문제는 주어진 하나의 입력에 대해 프로그램의 출력이 올바른지 결정하는 어려움이다.
- 예: 날씨 시뮬레이션이 "3일차 강우량: 12.3 mm"라고 예측할 때, 이것이 맞는지 알려면 일주일을 기다려야 하며, 그때조차 모델이 '틀린' 것인지 '근사'한 것인지 알기 어렵다.
- Implicit oracles (암묵적 오라클): 시스템 충돌, 무한 루프 등. 명백한 Failure만 감지한다.
- Explicit oracles (명시적 오라클): 형식적 명세, 이전 버전(Regression oracle) 등.
4. 테스팅 기법
4.1. Black-box vs. White-box

- Black-box (블랙박스): 테스터가 코드를 보지 않는다.
- White-box (화이트박스): 테스터가 코드를 본다.
- Gray-box (그레이박스): 부분적인 접근 권한을 갖는다.
4.2. Black-Box Testing

- 프로그램을 블랙박스로 간주하고 내부 구조를 무시한다. 명세에 따른 동작을 테스트한다.
- Functional Testing 또는 Behavioural Testing이라고도 한다.
- 테스트 데이터는 명세나 도메인 지식으로부터 도출된다.
- 접근 방식:
- Random Testing (무작위 테스팅)
- Equivalence Class Partitioning (ECP, 동등 클래스 분할)
- Boundary Value Analysis (BVA, 경계값 분석)
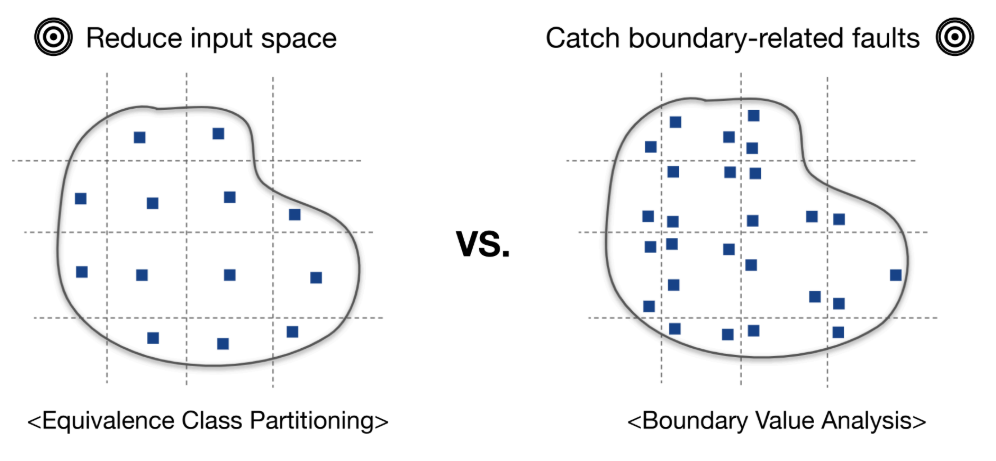
- ECP 예시: 사용자 나이
i(0~120). 보험 정책이 20, 70을 기준으로 나뉜다면, 유효 클래스 E1(0-20), E2(20-70), E3(70-120)과 유효하지 않은 클래스 U1(i<0), U2(i>120)로 분할한다. 각 클래스에서 하나씩 테스트 입력을 선택한다 (예: 200). - BVA 예시: 동일한 파티션에서 경계값을 테스트 입력으로 선택한다 (예: 121). BVA는
if (age < 20)같은 경계 결함을 잡는 데 효과적이다. - 파티셔닝의 한계: "동일한 동작"을 정의하는 방법이 모호하며, 파티셔닝 방법에 따라 효과가 달라질 수 있다.
isValidDate예제처럼 단순한 파티셔닝은 윤년 같은 복잡한 로직을 놓칠 수 있다. 테스터의 경험에 의존한다.
4.3. White-Box (Structural) Testing
- 소스 코드 구조에서 테스트를 설계하는 화이트박스 기법이다.
- 테스트의 적절성(adequacy)은 코드의 구조적 단위(라인, 브랜치 등)로 측정된다.
- 필수적이지만 충분하지는 않다.
5. Structural Coverage (구조적 커버리지)
5.1. 핵심 개념: Control Flow
- 테스트 적절성 측정은 두 가지 핵심 개념에 기반한다:
- Control-flow (제어 흐름): 어떤 경로가 실행되는가?
- Data-flow (데이터 흐름): 변수들이 경로를 따라 어떻게 되는가?
- Control Flow Graph (CFG): 프로그램의 그래프 표현. 노드는 문장(statements), 엣지는 실행 흐름을 나타낸다.
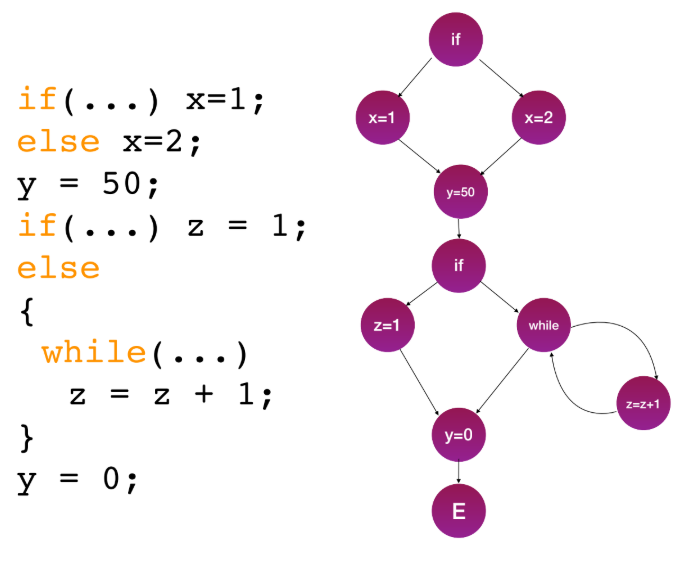
5.2. Code Coverage
- 테스팅을 언제 중단해야 하는가에 대한 완벽한 답은 없다. Code Coverage는 결함 탐지 능력과 상관관계가 있는 대리 측정치이다.
- 커버리지는 '무엇이 테스트되었는지'가 아니라 '무엇이 테스트되지 않았는지'를 보여준다.
- 필요하지만 충분하지 않은 조건이다 (실행되지 않은 라인의 결함은 감지 불가).
- 주의: 100% 커버리지가 모든 결함을 탐지했음을 의미하지 않으며, 커버리지 자체가 목표가 되면 안티패턴이 될 수 있다.
5.3. Control Flow 커버리지 기준
- Statement coverage (문장 커버리지): CFG의 노드(문장) 중 실행된 비율.
- Branch coverage (브랜치 커버리지): CFG의 분기 엣지 중 실행된 비율. (Decision Coverage라고도 함).
- Path coverage (경로 커버리지): CFG의 경로 중 실행된 비율.

- 경로 폭발 문제: 루프와 브랜치가 결합되면 경로 수가 기하급수적으로 증가한다. 예를 들어 바운드 k=20인 루프 1개는 개의 경로를 가질 수 있다. k 바운드의 루프 n개가 연속되면 개의 경로가 생긴다.
- 따라서 모든 경로를 테스트하는 것은 비현실적이며, 실제로는 더 간단한 기준(예: 브랜치 커버리지)을 사용한다.
5.4. 복잡한 커버리지 기준
- Decision Coverage (결정 커버리지):
if (x && (y || z))같은 전체 조건식이true와false모두로 평가되어야 한다. (Branch Coverage와 동일). - Condition Coverage (조건 커버리지):
x,y,z같은 각 개별 Boolean 하위 표현식이true와false모두로 평가되어야 한다. - Condition/Decision Coverage (C/DC): Decision Coverage와 Condition Coverage를 모두 만족해야 한다.
- Modified Condition/Decision Coverage (MC/DC): C/DC를 만족하면서, 각 개별 조건(Condition)이 다른 조건과 독립적으로 전체 결정(Decision)의 결과에 영향을 미침을 보여야 한다. (예: (1, 4)번 테스트 케이스 쌍으로
x의 독립적 영향을 확인).
5.5. Data Flow Analysis
- Control-flow가 "어디로 가는가"에 대한 것이라면, Data-flow는 "어떤 데이터를 가지고 가는가"에 대한 것이다.
- 변수의 정의(definition)와 사용(use)을 분석한다.
- CFG에 변수 사용을 표기한다:
d: definition (값 정의)u_p: predicate use (조건문에서 사용)u_c: computation use (계산에서 사용)k: kill (변수 소멸)
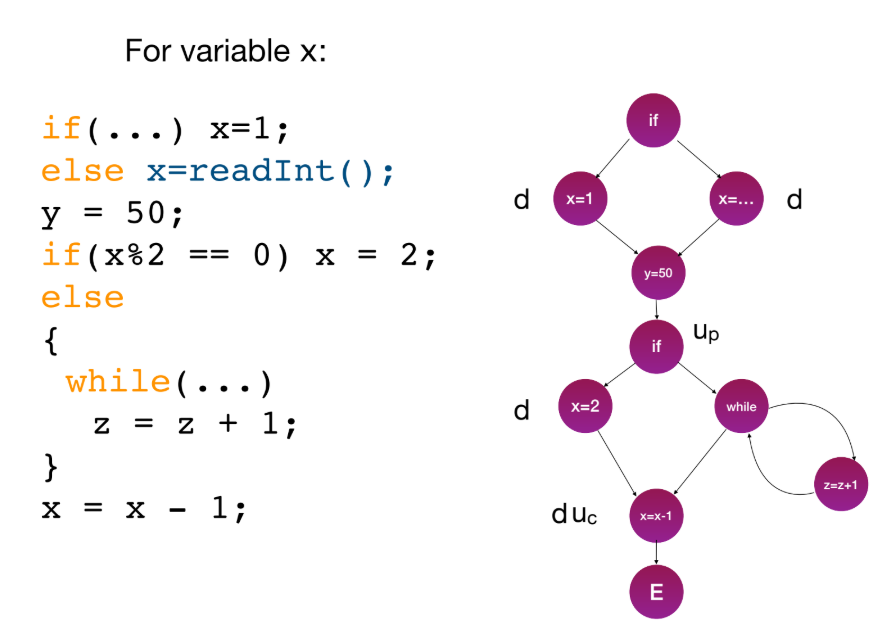
- Data-flow 패턴은 버그를 암시할 수 있다 (예:
ku(kill-then-use)는 버그).
5.6. Data Flow 커버리지 기준
- du-path: 변수
v에 대해,x노드에서의 정의(d)부터y노드에서의 사용(u)까지v가 재정의되지 않는(def-clear) 단순 경로(simple path)이다. - All DU Path Testing: 모든 정의
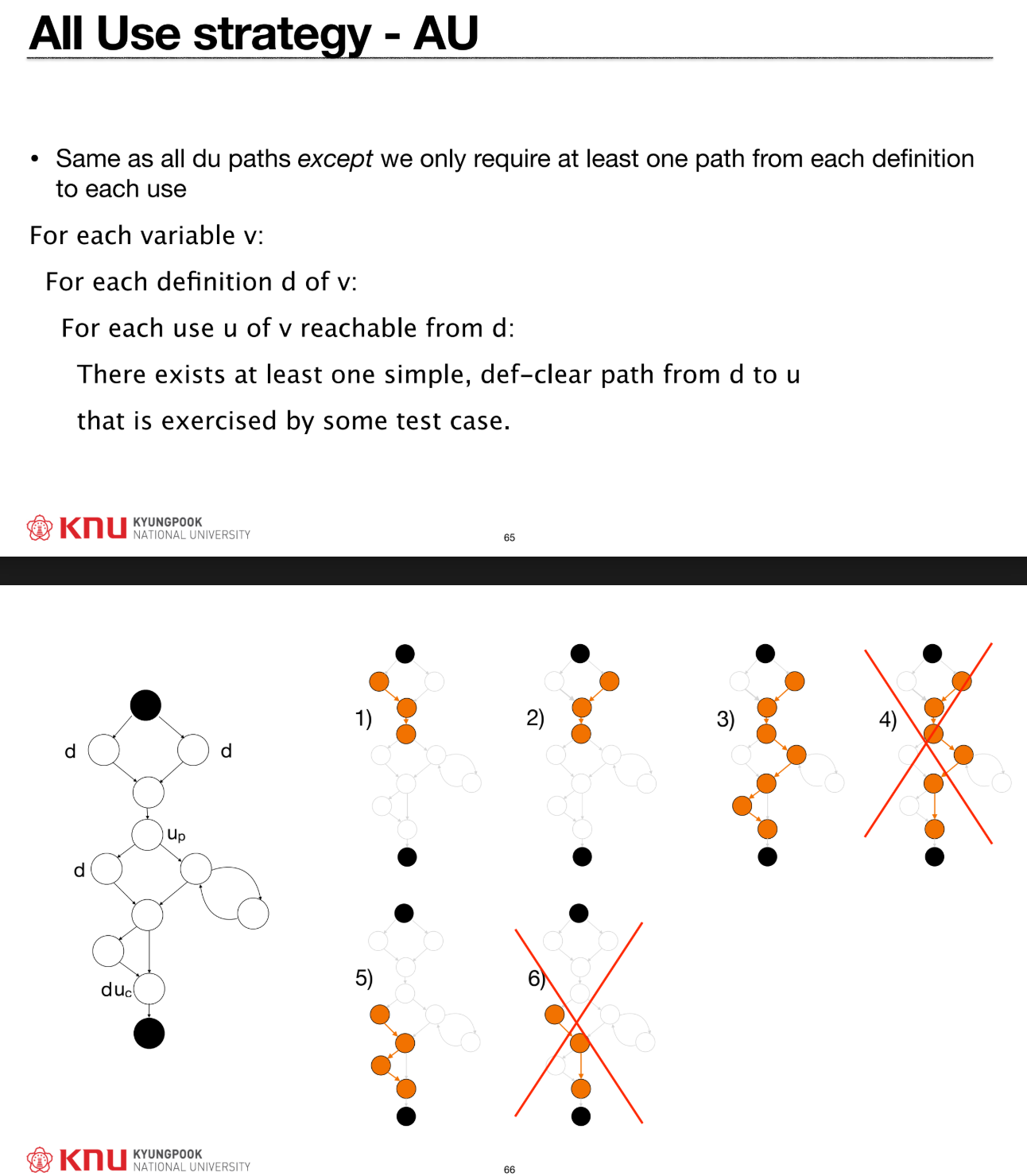
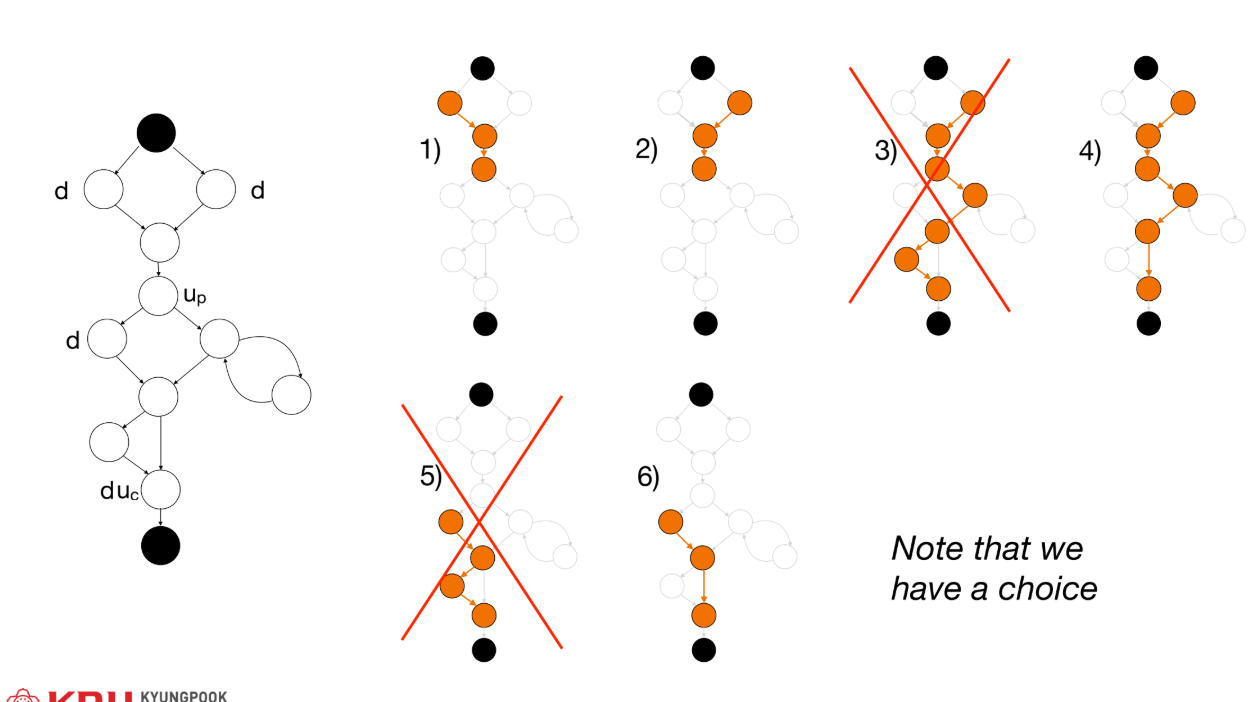
d에서 도달 가능한 모든 사용u까지의 모든 du-path를 실행해야 한다. - All Use (AU) Strategy: 모든
d에서u까지 적어도 하나의 du-path를 실행해야 한다. (더 약한 기준).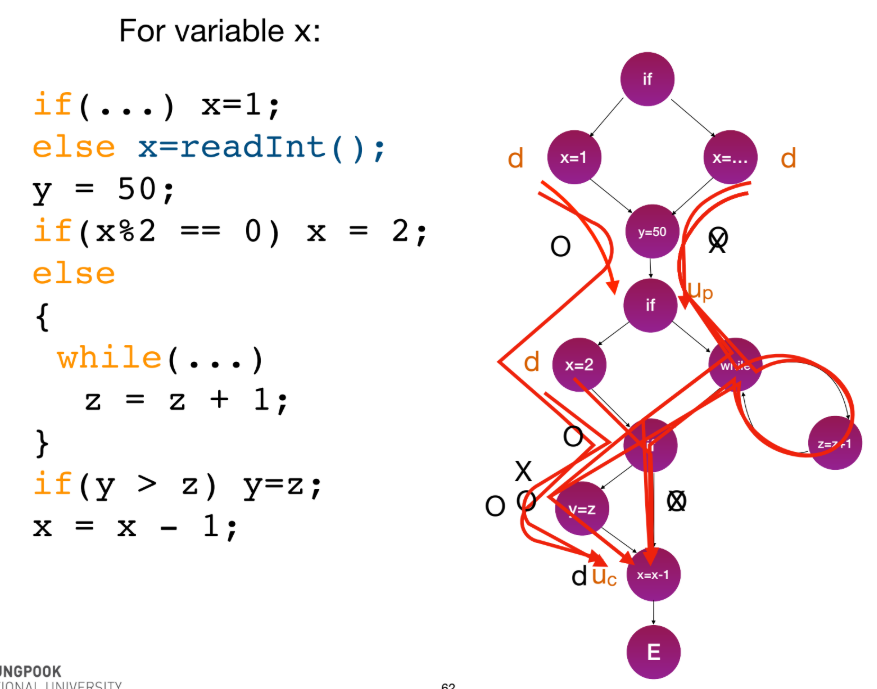

- Data-flow 테스팅의 한계: 초기화되지 않은 사용(
ku) 등은 잡을 수 있지만,x*2를x*3로 잘못 쓴 것과 같은 의미론적(semantic) 버그나 논리 오류는 감지할 수 없다.
5.7. 권장 실습 및 커버리지 측정
- (1) Control-flow (문장, 브랜치)로 시작 -> (2) Data-flow (All-Uses 등) 적용 -> (3) Oracle, Assertion 등 의미론적 검사 확장.
- 커버리지는 코드를 실행할 때 도달한 부분을 수집하기 위해 추가 코드를 삽입하는 Coverage Instrumentation을 통해 측정된다.
- 도구:
gcov(C),Jacoco(Java),coverage.py(Python) 등.
5.8. 테스팅 레벨
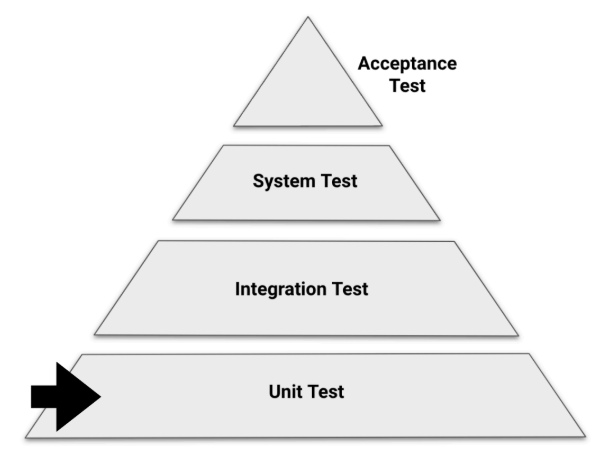
- Unit Test (단위 테스트): 개별 컴포넌트/함수. (Structural testing이 가장 관련 높음).
- Integration Test (통합 테스트): 컴포넌트 간 상호작용.
- System Test (시스템 테스트): 전체 시스템을 요구사항과 비교.
- Acceptance Test (인수 테스트): 사용자 요구/비즈니스 목표 검증.
- 업계 현황: 항공 전자 산업 등 일부는 100% 커버리지를 요구하지만, 실제로는 75-80%가 허용되기도 한다. (연구에 따르면 효과적인 결함 탐지를 위해 90% 이상이 필요할 수 있음).
6. 자동화된 테스트 데이터 생성
6.1. Path Condition (경로 조건)
- 커버리지 달성을 위한 테스트 입력 생성을 자동화하는 것이 목표이다.
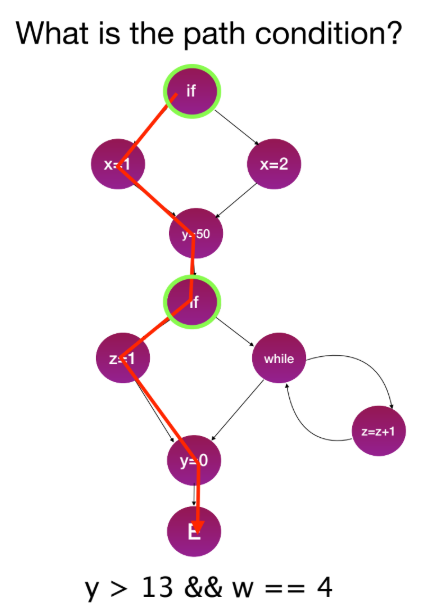
- Path Condition: 프로그램 실행을 특정 경로로 유도하는 조건(predicate)의 집합이다. (예:
y > 13 && w == 4). - 이 Path Condition을 만족하는 입력값을 찾으면 해당 경로가 커버된다.
6.2. Search-Based Testing (SBT)
- SBT (탐색 기반 테스팅): Path Condition을 Fitness Function (적합도 함수)으로 변환하고, 메타휴리스틱 탐색(최적화)을 사용해 이 함수를 최소/최대화하는 입력값을 찾는다.
- Fitness Function (브랜치 커버리지용): Fitness = [Approach Level] + normalize([Branch Distance]).
- Approach Level (접근 수준): 목표(target) 브랜치에 도달하기 위해 통과하지 못한(막힌) 중첩 레벨(if문)의 수.
- Branch Distance (브랜치 거리): 경로를 막은 마지막 조건문을 얼마나 근소한 차이로 만족시키지 못했는지를 나타내는 값.
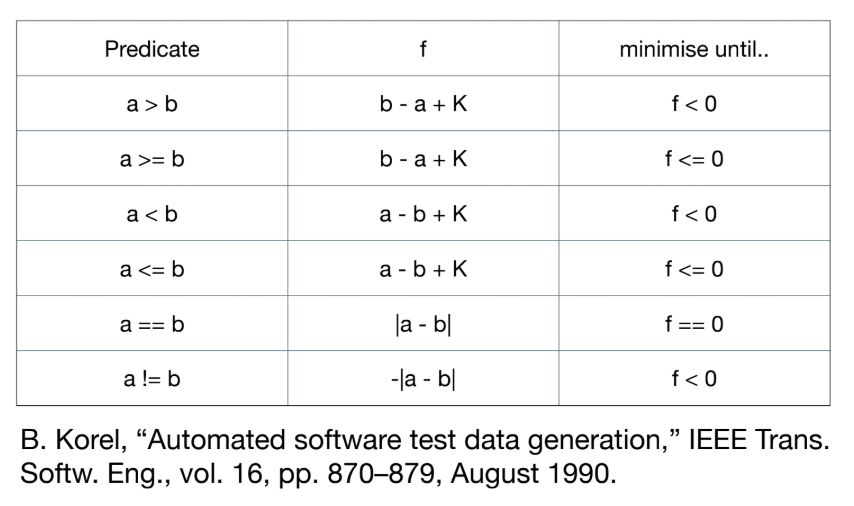
- 예:
a == b를 만족시키려면f = |a-b|를 0으로 최소화한다.a >= b를 만족시키려면f** = b - a + K를 0 이하로 최소화한다. 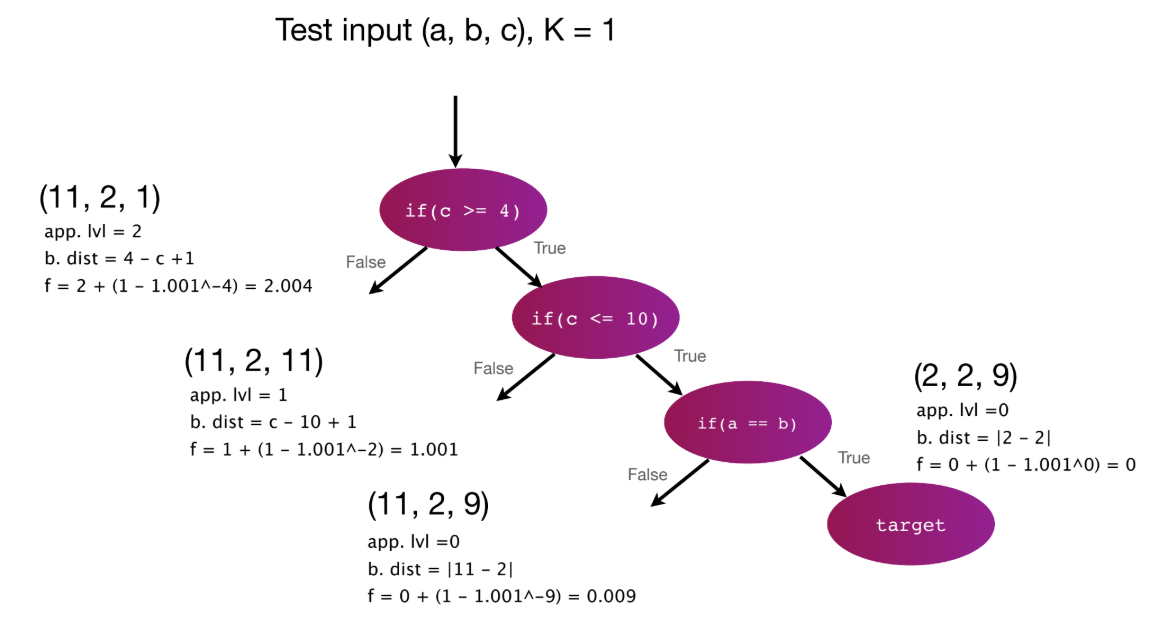
- 정규화 (Normalization): Branch Distance(임의의 큰 값 가능)보다 Approach Level(작은 정수)을 우선하기 위해 Branch Distance를 [0, 1) 범위로 정규화한다.
- 탐색 알고리즘:
- Hill Climbing: 한 번에 하나의 해(solution)를 사용하며, 현재 해보다 더 나은 Fitness를 가진 이웃(neighbour)으로 이동한다.

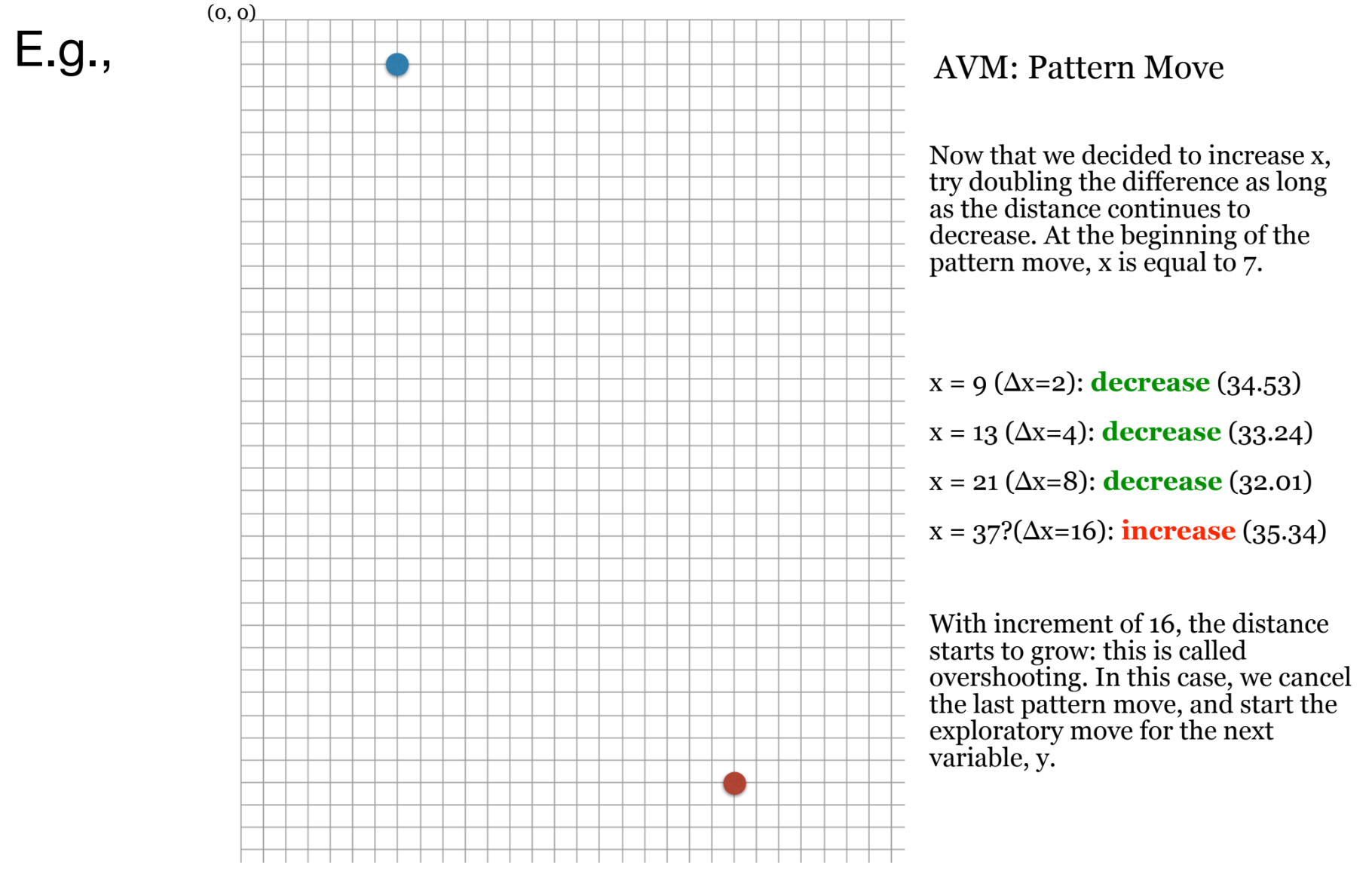
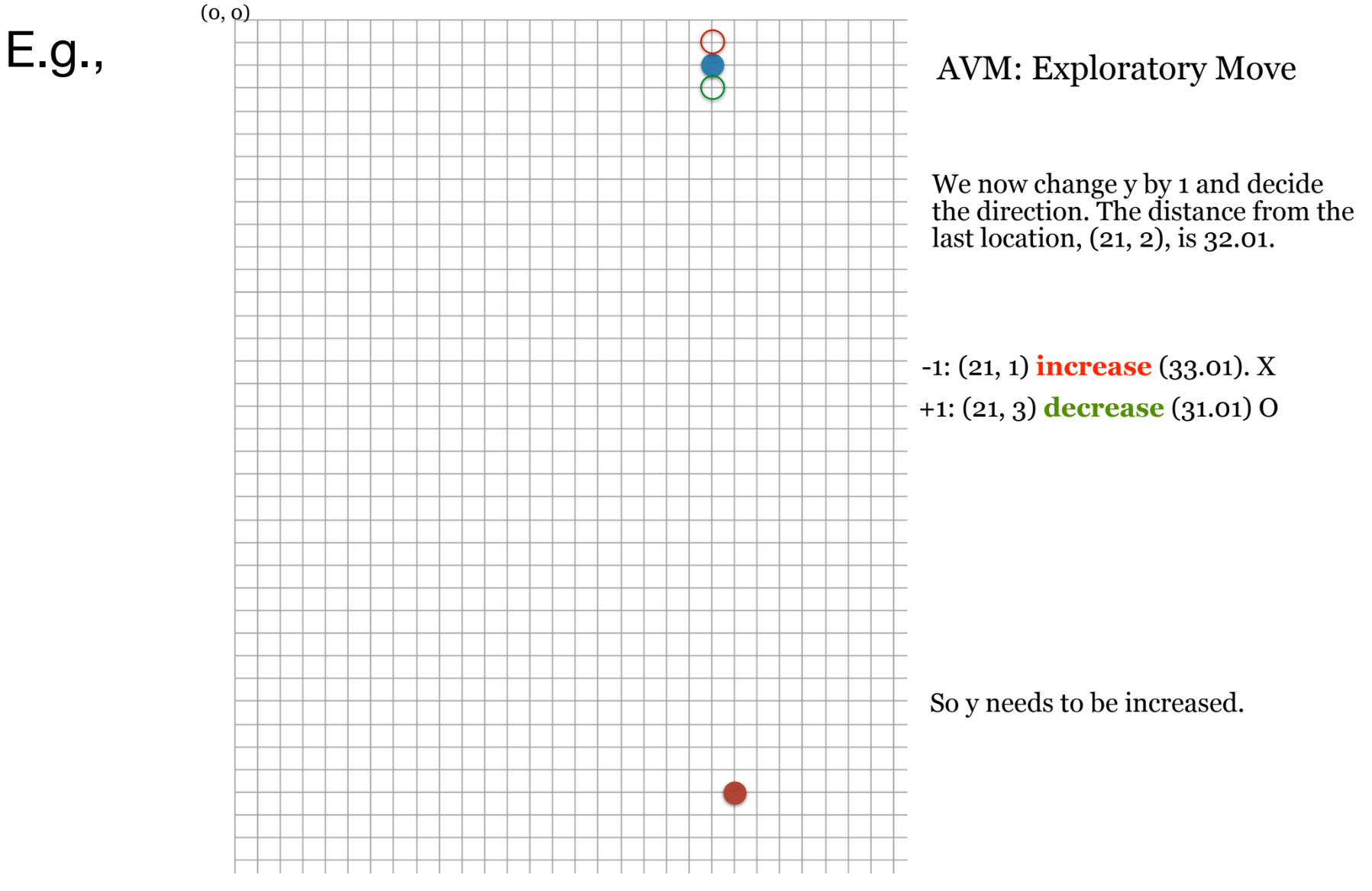
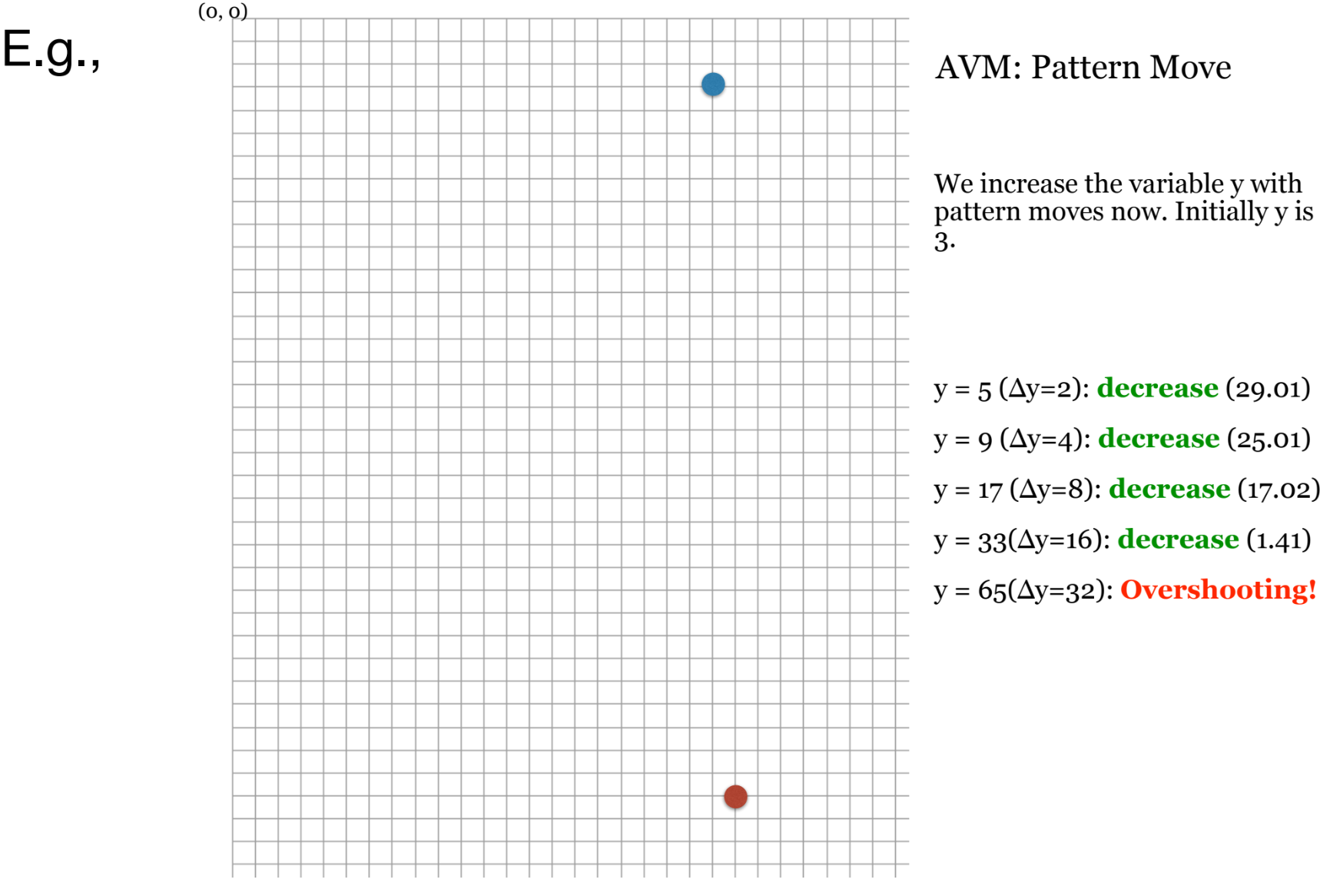
- Alternating Variable Method (AVM): 한 번에 하나의 변수만 변경해보며 Fitness가 개선되는 방향을 찾는 로컬 탐색.
- Evolutionary Testing (진화형 테스팅): 하나의 해가 아닌 개체군(population)을 사용한다.
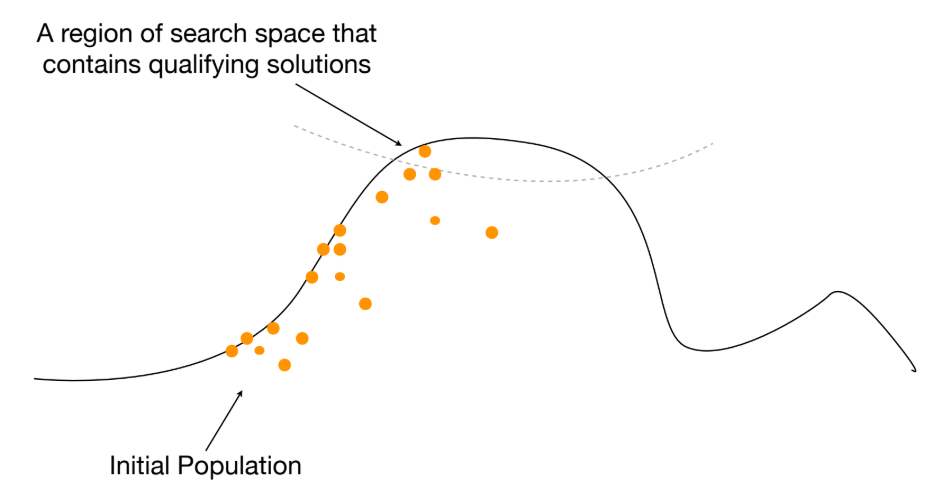
- SBT의 장단점: 비구조적 기준(예: 스트레스 테스팅)에도 적용 가능하지만, "거리"(Fitness) 정의가 어렵고 시간이 오래 걸릴 수 있다.
6.3. Dynamic Symbolic Execution (DSE)
- DSE (동적 심볼릭 실행) / Concolic Testing:
- 기본(무작위) 입력으로 프로그램을 실행하고 Path Condition을 수집한다.
- 수집된 Path Condition의 마지막 절(clause)을 부정(negate)한다.
- 새로운 Path Condition을 Constraint Solver (제약 조건 해결기)에 전달하여 이를 만족하는 새로운 입력값을 찾는다.
- 새 입력값으로 다시 실행하여 새로운 경로를 탐색한다 (반복).
![p.92: DSE가 testme(int[] a) 함수의 경로를 탐색하는 과정 (트리 및 테이블)](/assets/images/Pasted image 20251022204053-7cfad0921ef52b75fd5b3c4575f9ca8a.png)
- (입력
null) -> PC:a == null - (부정 후 해결
a != null-> 입력{}) -> PC:a != null && !(a.length > 0) - (부정 후 해결
a != null && a.length > 0-> 입력{0}) -> PC:a != null && a.length > 0 && a[0] != 42 - (부정 후 해결
a != null && a.length > 0 && a[0] == 42-> 입력{42}) -> 버그 발견.
- (입력
- DSE의 장단점: 매우 빠르고 효과적이지만, Constraint Solver의 성능에 전적으로 의존한다. Solver는 부동 소수점(floating point) 계산(반올림 문제) 등에서 어려움을 겪을 수 있다.
7. 요약
- 커버리지는 충분한 목표는 아니지만, 달성하기 어렵다.
- 자동화된 테스트 입력 생성은 커버리지라는 구체적이고 자동화 가능한 목표를 제공하여 도움을 준다.
- DSE (SMT solvers)와 SBT (metaheuristic optimisation) 같은 기술이 이를 위해 적용된다.
- 하지만 자동화된 테스팅에서 진짜 어려운 문제는 여전히 Test Oracle 문제에 있다.
Team 0 발표 준비
Identifying BugInducing Commits by Combining Fault Localisation and Code Change Histories
V. Eveluation Setup
- FONTE 기법의 평가를 위해 사용된 데이터셋
- FONTE의 구현 세부사항
- Research Questions와 Research Protocol
A. Dataset of Bug Inducing Commits
- 기반 데이터셋: Defects4J v2.0.0 사용
- Java Opensource에서 발견된 835개의 실제 Bug 모음
- Bug를 드러내는 Test Suite와 전체 Commit List를 제공하나 각 Bug에 대한 Bug Inducing Commit 정보는 부족
- 초기 BIC Dataset: Wen et al.이 구축한 91개의 Defects4J Bug에 대한 BIC Dataset 중 67개의 Ground-Truth BIC로 시작.
- 9개는 SVN을 사용하여 Git 기반인 FONTE에서 추적할 수 없어 제외
- 이전 연구에서 부정확하다고 밝혀진 14개와 코드 변경 없이 라이선스 주석만 변경된 1개 제외
- 증강 Dataset: 평가 Dataset을 확장하기 위해 두 저자가 독립적으로 추가적인 Ground-Truth BIC를 수동으로 선별
- BIC 검색 공간이 10개 이하인 Bug들을 우선적으로 검토하여 70개 사례에 대해 합의
- 추가적으로 76개의 Data Point를 더 포함하여 총 206개(67+146-7(중복))개의 Data Point를 평가에 사용
- Project별 분포: Lang, Math, Closure Prject가 다수 차지
B. Implementation Details of FONTE
- 기본 속성
- 세분성: Statement Level에서 FONTE를 적용 는 Program의 Statement Set
- Initial Search Space(): 첫 Commit부터 Bug Version Commit까지 모두 포함
- Test Cases(): Bug를 드러내는 TC()와 그 관련된(Relevant) TC만 사용
관련 Test는 실패하는 TC가 실행하는 Class 중 적어도 하나의 이름이 TC의 전체 이름에 포함되는 경우로 정의
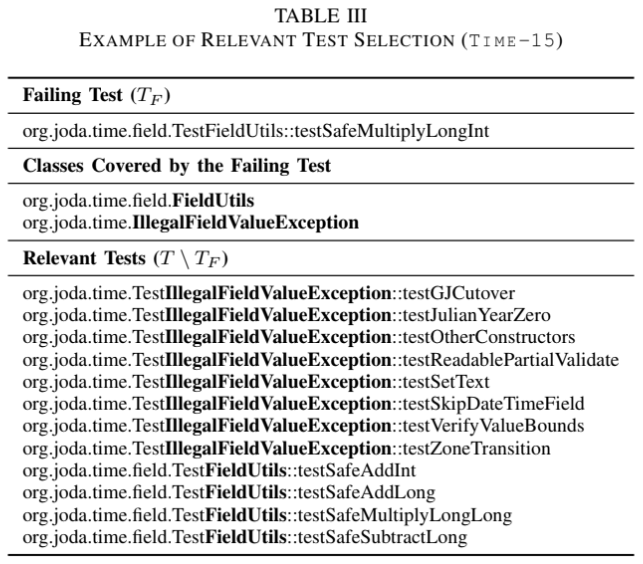
- Cover Relation 구성: 와 간의 Cover Relation을 구축하기 위해 Defects4J에 포함된 Cobertura v2.0.3을 사용하여 Statement Level의 Coverage 측정
- Evolve Relation 구성: 와 간의 Evolve Relation을 확립하기 위해 git log command를 사용
- git log 외에도 CodeShovel 및 CodeTracker와 같은 도구도 사용
- Overhead 방지: Statement의 Commit List를 찾는 대신 해당 Statement를 포함하는 Method의 Commit List를 추적하여 높은 재현율을 보장하고, Omission Bug에도 대응
- Semantic-Preserving Commits 탐지
- 코드 표준 통일: AST를 비교하기 전 OpenRewrite v7.21.0을 사용하여 CheckStyle 규칙을 위반하는 Error를 수정하는 Cleanup Receipe를 적용함으로 두 Version File 간 코딩 표준을 일치
- AST 비교: Formatting 후 GumTree v3.0.0의 Isomorphism Test를 사용하여 AST를 비교
- Fault Localisation
- FONTE에 Plugin할 수 있는 두 가지 대표적인 FL 기법을 사용
- SBFL(Spectrum-Based Fault Localisation): 널리 사용되는 Ochiai Formula 사용
- IRFL(Information Retrieval-based Fault Localisation): Blues라는 Non-supervised Statement Level IRFL 기법을 사용하며, Defects4J Bug에 대해 미리 계산된 점수를 활용
- FONTE에 Plugin할 수 있는 두 가지 대표적인 FL 기법을 사용
- Hyperparameter
- Rank-based 투표력():
- 동점 처리 방식():
- 깊이 기반 감쇠(decay factor, ):
C. Resarch Questions
- RQ1. FONTE는 BIC를 얼마나 정확하게 찾는가?
- RQ2. FONTE는 다른 BIC 식별 접근 방식보다 우수한가?
- RQ3. Weighted Bisection은 Standard Bisection에 비해 얼마나 효율ㅈ거인가?
VI. Results
A. RQ1. Effectiveness of TONTE
RQ1-1. Search Space Reduction
- 평가 프로토콜: Stage 1과 Stage 2 후의 BIC Search Space 감소 비율을 계산
- git log, CodeShovel, CodeTracker의 세 가지 코드 이력 추적 도구를 사용해 결과 비교
- 결과
- 감소 비율: 평균적으로 BIC Search Space는 초기 크기의 11%로 축소
- 도구 선택에 따른 감소 비율의 영향은 미미
- 유효성 비율: 실제 BIC가 축소된 검색 공간 내에 포함될 비율
- git log가 100%로 가장 신뢰성이 높았으며, CodeShovel은 99%, Code Tracker는 98.5%
- 소요 시간: git log가 평균 27.3초로 가장 빠름
- 감소 비율: 평균적으로 BIC Search Space는 초기 크기의 11%로 축소
- 결론: git log가 신뢰성 및 효율성 면에서 가장 우수하며, BIC Search Space는 11%로 효과적으로 축소됨
RQ1-2. Ranking Perfomance
- 평가 프로토콜: FONTE의 성능을 평가하기 위해 Mean Reciprocal Rank(MRR)와 Accuracy@n(Acc@n, 상위 n개의 순위 내 BIC가 포함될 비율) 두 가지 순위 기반 지표 사용
- git log를 Evolve Relation 구축에 사용하고, SBFL(Ochiai) 또는 IRFL(Blues)을 기본 FL 기법으로 다양한 Hyperparameter 설정과 조합하여 평가
- 결과
- 랜덤 기준선 대비 우수성: 모든 설정에서 FONTE는 랜덤 기준선보다 월등히 뛰어난 성능을 보임
- 최고 성능: SBFL과 결합했을 때 FONTE는 가장 좋은 성능을 달성
- 최고 MRR: 0.481(SBFL, )
- 최고 Acc@1: 32.0%(SBFL, )
- 최고 Acc@5: 70.4%(SBFL, ) or (SBFL, )
- Hyperparameter 영향: 설정이 다른 값에 비해 일관되게 우수
- FL 기법 영향: SBFL과 결합한 FONTE가 IRFL과 결합한 FONTE보다 우수
- SBFL의 FL 정확도가 IRFL보다 높기 때문
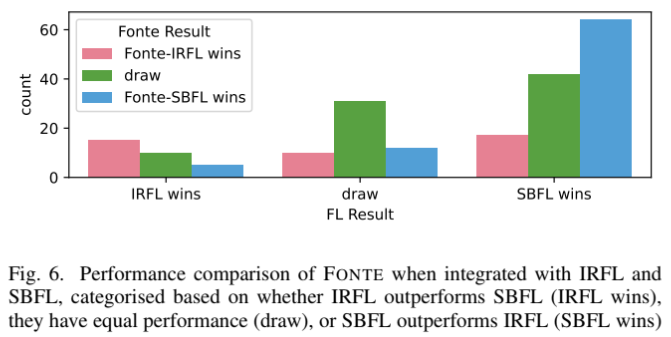
- SBFL의 FL 정확도가 IRFL보다 높기 때문
- 결론: FONTE는 축소된 Search Space 내에서 BIC를 식별하는 데 높은 효과를 보이며, SBFL과 결합했을 때 MRR 0.481을 달성하며 실제 BIC를 후보군 내에서 상위권에 Rank시키는 능력을 입증
RQ1-3. Ablation Study
- 평가 프로토콜: FONTE의 핵심 기능인 Rank-based Voting Power와 Depth-based Decay의 영향 조사를 위해 각 기능을 제거하거나 모두 제거했을 때 성능 비교
- Rank-based Voting Power 제거: FL 점수를 그대로 Voting Power로 사용
- Depth-based Decay 제거:
- 결과
- Rank-based Voting Power 제거: FONTE-IRFL에서 10.8%, FONTE-SBFL에서 7.3%의 MRR 감소
- Depth-based Decay 제거: FONTE-IRFL에서 6.8%, FONTE-SBFL에서 7.3%의 MRR 감소
- 모두 제거: FONTE-IRFL에서 16.6%, FONTE-SBFL에서 13.9%의 MRR 감소
- 결론: Rank-based Voting Power와 Depth-based Decay는 FONTE의 효과에 중요한 역할을 하며, 두 기능을 모두 제거할 경우 MRR이 최대 16.6%까지 감소 Rank-based Voting Power가 Depth-based Decay보다 성능 향상에 더 핵심적인 역할을 함
B. RQ2. Comparison with Other Techniques
- 평가 프로토콜: FONTE의 BIC Ranking 성능을 다른 Commit Score 기준선과 비교
모든 기법은 FONTE와 동일한 축소된 Search Space 내에서 평가
- MAX Aggregation of FL Scores: Commit이 변경한 모든 Code Element 중 가장 높은 FL 점수를 Commit Score로 할당
- Bug2Commit: 상태 기반 IR 기반 BIC 식별 기법으로, Commit Message, 변경 파일 이름, Bug Report 내용을 기반으로 점수를 할당
- FBL-BERT: BERT 기반 Change set 위치 파악 기법, Bug Report를 입력으로 사용
- 결과
- FONTE는 모든 평가 지표에서 기준선보다 뛰어난 성능 보임.
- MRR 비교: FONTE-SBFL은 기준선 대비 최소 45.8% (Bug2Commit 대비), FONTE-IRFL은 최소 37.3% (Bug2Commit 대비) 더 높은 MRR 달성
- IRFL 기반 비교: 동일하게 버그 보고서( 표시된 기법)를 입력 데이터로 사용하는 다른 기법들보다 FONTE-IRFL이 훨씬 우수한 성능 보임 FONTE의 코드 수준 FL 점수를 커밋 수준으로 변환하는 접근 방식의 효과 입증
- 결론: FONTE의 점수 부여 접근 방식은 FL 점수에 대한 최대 집계 방법과 최신 IR 기반 기법 모두 능가함 IRFL과 짝을 이룬 FONTE는 동일한 입력 데이터를 활용하는 다른 방법보다 우수한 결과 달성
C. RQ3. Standard Bisection vs. Weighted Bisection (표준 이분법 대 가중 이분법)
- 평가 프로토콜: 버그 탐지 테스트가 완벽하게 작동한다고 가정하고 표준 이분법과 FONTE에서 생성한 점수를 활용하는 가중 이분법을 시뮬레이션
- 가장 성능이 좋았던 FONTE-SBFL 설정()의 커밋 점수 사용
- 결과
- 전체 커밋 이력 () 대상: 가중 이분법은 대상 버그의 약 98%(206개 중 202개)에서 검색 비용을 줄였으며, 평균 6.3회의 반복 절약, 성능이 저하 없음

- 축소된 커밋 이력 () 대상: 가중 이분법은 65%의 경우(133/206)에서 반복 횟수 절약, 27.2%는 동일, 단지 8.3%의 경우(17/206)에서만 반복 횟수 증가

- 상관 관계: 가중 이분법의 효과는 FONTE가 BIC를 더 높은 순위로 정확하게 랭크할수록 더 좋음
BIC의 정규화된 순위와 절약된 반복 횟수 사이에 -0.64의 Pearson 상관 계수 관찰됨
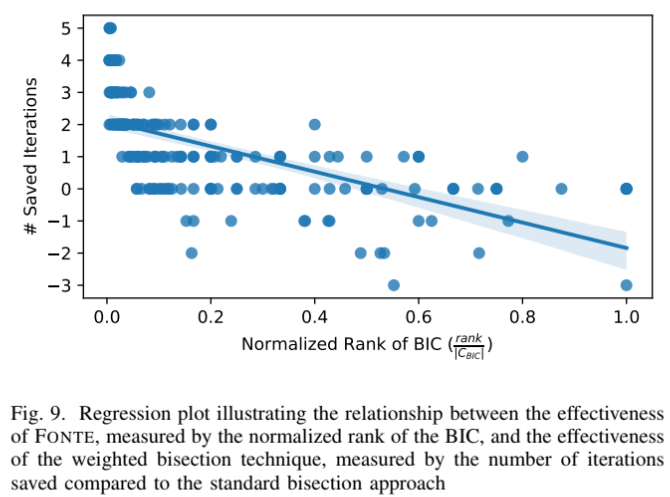
- 통계적 유의성: Wilcoxon signed-rank test 결과, p-value 로 가중 이분법이 반복 횟수를 절약하는 성능 향상이 통계적으로 유의미함을 확인
- 전체 커밋 이력 () 대상: 가중 이분법은 대상 버그의 약 98%(206개 중 202개)에서 검색 비용을 줄였으며, 평균 6.3회의 반복 절약, 성능이 저하 없음
- 결론: 가중 이분법과 FONTE 점수를 결합하면 전체 커밋 이력을 대상으로 할 경우 98%의 버그에서 BIC 검색 비용 절감이 가능, 평균 6.3회의 반복 절약 축소된 후보 커밋 집합 내에서도 65%의 경우에서 검색 반복 횟수 절약해 효율적인 검색 프로세스 제공
IX. Related Work
A. Information Retrieval-based BIC Identification (정보 검색 기반 BIC 식별)
- Locus: 버그 보고서를 입력 쿼리로 사용하여 토큰 유사성을 기반으로 관련 변경 덩어리(change hunk)를 찾은 최초의 연구
- Orca: 예외 메시지나 고객 불만과 같은 버그 증상을 입력으로 받아 파일 수준의 FL 점수(TF-IQF)를 계산하고, 이를 커밋 수준으로 집계한 후 기계 학습을 사용하여 커밋의 위험도를 예측하여 순위를 매김
- Bug2Commit: 커밋과 버그 보고서에서 추출된 여러 특징을 사용하고 벡터 표현의 평균을 취하여 집계 Non-supervised Learning이지만, 단어 임베딩 모델을 훈련하기 위해 Project 별 과거 데이터 필요
- FBL-BERT: 사전 훈련된 BERT 모델을 미세 조정해 버그 보고서에 대한 관련 변경 집합을 검색
FONTE와의 주요 차이점:
- FONTE는 훈련이 필요 없음
- FONTE는 테스트 실행의 Coverage를 활용하여 코드 수준의 FL 점수를 생성하고, 이를 커밋 이력을 통해 시간적 영역(Temporal domain)으로 확장 텍스트 정보에만 의존하는 IR 기반 기법의 한계 극복 실패를 재현할 수 없는 경우 IR 기반 기법이 사용될 수 있지만, Coverage가 가능한 경우 FONTE가 더 정확하게 순위를 매길 수 있음
B. Other BIC Identification Techniques (기타 BIC 식별 기법)
- SZZ 알고리즘 및 변형: 버그 수정 커밋(Bug Fixing Commit, BFC)을 입력으로 필요로 하므로 디버깅 시점에는 적용 불가
- ChangeLocator: 충돌(crash) 보고서의 호출 스택 정보를 사용하여 충돌 유발 변경 사항을 찾는 학습 기반 접근 방식 FONTE는 충돌에 국한되지 않고 일반적인 실패에도 적용 가능
- FACF(Flaky Aware Culprit Finding): 가중 이분법과 유사하게 베이즈 추론을 기반으로 비결정적인 테스트(flaky test) 환경에서 이분법 프로세스 안내 FONTE는 커밋 점수를 초기 확률 분포로 사용하여 이분법을 안내하며, FACF는 이 초기 정보를 활용 가능
C. Highly Related Works (매우 관련이 높은 연구)
- FaultLocator: 코드 수준의 FL 점수를 사용하여 실패 유발 원자 편집(atomic edits) 식별 FONTE는 커밋 이력에서 BIC를 찾는 것이 목표인 반면, FaultLocator는 두 버전 사이의 편집 내용 식별
- WhoseFault: 코드 수준 FL 점수와 커밋 이력을 사용하여 버그 담당 개발자를 결정하는 방법 BIC 식별을 직접 목표로 하지 않기 때문에 FONTE와 직접 비교 및 통합 불가 FONTE는 BIC를 정확히 식별함으로써 변경 사항의 작성자 정보를 기반으로 버그 담당 개발자를 찾는 데에도 활용 가능